A Chaotic Pendulum in Phase Space with Java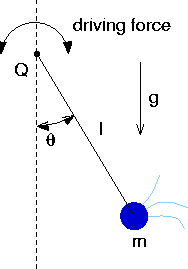

Suggested Explorations

1. Try out all the tabulated cases and describe what's happening.
2. Compare the motion of the two almost-identical pendula, and pick out a particular point where the coordinate space motions begin to differ.
3. Compare the motion of the two almost-identical pendula, and note in which way the phase-space motion of the two pendula appear similar even though the coordinate space motions differ.
4. Turn off the frictional and driving torques and identify the phase-space figures which correspond to the natural oscillations of the system.
5. Describe how the phase-space shapes of the natural oscillations change as the initial velocity is made greater and greater.
6. Turn off the driving torque, but not friction, and describe the shape of the phase-space figures.
7. Identify which physical motions of the pendulum lead to particular shapes in phase space.
8. In what direction (clockwise or counter clockwise) does the pendulum travel in phase space?
9. What happens in phase space when the pendulum goes "over the top" in coordinate space?
10. How can you tell in phase space if the pendulum is swinging clockwise or counter clockwise in coordinate space?
11. Identify which parts of the orbit are transients and which parts are attractors.
12. Try to find a limit cycle in which the average energy put into the system during one cycle exactly balances the average energy dissipated by friction during that cycle.
13. Make the driving torque so large that it overpowers the natural oscillations of the pendulum and the steady-state motion is at the frequency of the driver. This is an example of mode locking.
14. Sweep the driver's frequency through the pendulum's natural frequency and find resonances.
15. Turn off friction and again sweep the driver's frequency through the pendulum's natural frequency and find resonances.
16. Look for resonances which also occur when the ratio of driver's frequency to natural frequency is the ratio of integers.