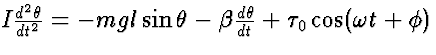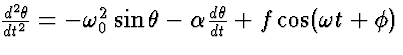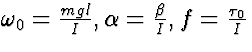A Chaotic Pendulum in Phase Space with Java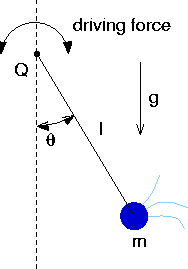figure of pendulum

Equation of Motion

A pendulum is displaced from the vertical by an angle theta, and moves through a viscous medium with frictional coefficient beta. An external, periodic torque is also applied to the pendulum. Although simple, this system displays chaotic behavior (similar to that in which the pivot point of the pendulum is made to oscillate). Newton's laws of rotational dynamics tells us that the moment of inertia I times the angular acceleration equals the sum of torques due to gravity, friction, and driver:

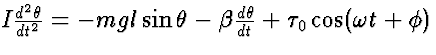$I {d^2\theta \over dt^2} = -mgl\sin\theta -\beta {d\theta\over dt} +\tau_0\cos(\omega t + \phi) $
We divide by the moment of inertia to obtain a second order, nonlinear, ordinary differential equation in standard form:
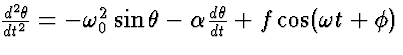${d^2\theta \over dt^2} = -\omega_0^2\sin\theta -\alpha {d\theta\over dt} +f \cos(\omega t + \phi) $
where omega without a subscript is for the external driver and the other constants are

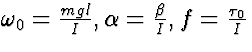
$\omega_0 = {mgl\over I}, \alpha= {\beta\over I}, f = {\tau_0\over I}$

Next: What are Pendulum Applets
Back: Main Page