
The theory is the physics of "Statics" and is covered in Chapter
5 Forces in Equilibrium of the
High
School Physics Manual written by Pat Canan and now being placed on
the Web.
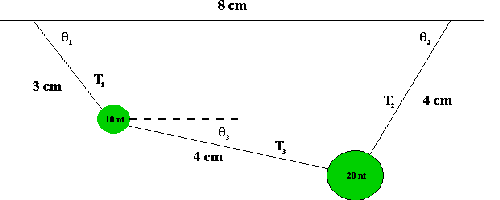
The geometry in the figure yields two equations and the balance of the
forces in the horizontal and vertical directions add another four:
![]()
![]()
![]()
![]()
![]()
![]()
We now can see a "problem". There are six equations here with three unknown tensions, three unknown sine functions, and three unknown cosine functions, for a total of nine unknowns. You cannot solve simultaneous equations when there are more unknowns than equations. Okay, we have been a little too dramatic; there is the trigonometric identity
sin A sin A + cos A cos A =1,
where A stands for one of the angles in the figure. When applied
to the three angles in the problem, this identity leaves us with nine simultaneous
equations in nine unknowns.
Now we see the real problem. In general, these simultaneous equations cannot
be solved by algebraic techniques (unless you are ingeniously clever or
lucky) because they are involve more than just the first power of the unknowns.
They are thus "nonlinear" or "transcendental" equations.