Applying Newton's second law for rotations to a pendulum results in a nonlinear second order differential equation,
If the displacement is small we can set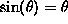 
(we use a Taylor
series of first order) and get our old friend, the harmonic oscillator.
However, there is no problem solving the exact differential equation numerically. We just take the Runge-Kutta algorithm and include the sine function in the definition of the derivatives, resulting in the following set of equations.
