Water Dielectric and Microwave Radiation^a

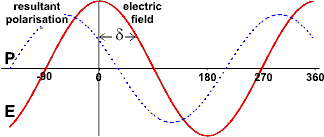
The water dipole^b attempts to continuously reorient in electromagnetic radiation's oscillating electric field (see external applet). Dependent on the frequency the dipole may move in time to the field, lag behind it or remain apparently unaffected. When the dipole lags behind the field then interactions between the dipole and the field leads to an energy loss by heating, the extent of which is dependent on the phase difference of these fields; heating being maximal twice each cycle [455]. The ease of the movement depends on the viscosity and the mobility of the electron clouds. In water these, in turn, depend on the strength and extent of the hydrogen bonded network. In free liquid water this movement occurs at GHz frequencies (microwaves) whereas in more restricted 'bound' water it occurs at MHz frequencies (short radiowaves) and in ice at kHz frequencies (long radiowaves). The re-orientation process may be modeled using a 'wait-and-switch' process where the water molecule has to wait for a period of time until favorable orientation of neighboring molecules occurs and then the hydrogen bonds switch to the new molecule [343]. Microwave heating has been modeled using the TIP4P-FQ potenial [570].

The applied field potential (E, volts) of electromagnetic radiation is given by;

E = E_max.cos(ωτ)

where E_max is the amplitude of the potential, ω is the angular frequency in radians.second^-1 and t is the time (seconds). If the polarization lags behind the field by the phase (δ, radians)

then the polarization (P, coulombs) varies as P = Pmax.cos(ωt - δ) where Pmax is the maximum value of the polarization.

Hence the current (I, amperes) varies as

I = (dP/dt) = -ωP_max.sin(ωτ - δ)

The power (P, watts) given out as heat is the average value of (current x potential). This is zero if there is no lag (i.e. if δ = 0), otherwise 

P = 0.5 P_maxE_maxω.sin(δ)

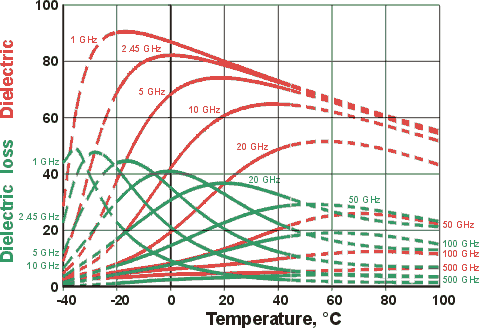
It is convenient to express the dielectric constant in terms of a complex number (ε_r*, complex dielectric permittivity) defined as:

ε_r* = ε_r´ - iLf 

Where ε_r´ is the ability of the material to be polarized by the external electric field, Lf (the loss factor) quantifies the efficiency with which the electromagnetic energy is converted to heat and i = 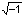. This equation may be visualised by considering the total current is the vector sum of the charging current and the loss current; the angle δ as the phase difference (lag) between the electric field and the resultant (orientation) polarisation of the material (see similar treatment in rheology).

tan(δ) = loss current/charging current = Lf/εr´ (see derivation)

The terms (ε_r*, ε_r´, Lf ) are all affected by the frequency of radiation; the relative permittivity (ε_r´, dielectric constant) at low frequencies (ε_S, static region^d) and at high ( visible) frequencies the (ε_∞, optical permittivity) are the limiting values. The relative permittivity changes with the wavelength (and hence frequency):

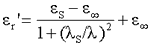
where ε_S is the relative permittivity at low frequencies (static region), and λ_S is the critical wavelength (maximum dielectric loss).

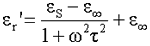                 (see more on complex dielectric permittivity)

where τ is the relaxation time (a measure of the time required for water to rotate (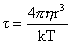where  r is the molecular radius, k is the Boltzman constant and η is the viscosity), also considered as the delay for the particles to respond to the field change, or for reversion after disorientation. The maximum loss occurs when ω = 1/τ ^c. For water at 25°C, τ is 8.27 ps and r is half the (diffraction-determined) inter-oxygen distance (1.4 Å).

Figure 1. Dielectric permittivity and dielectric loss of water between 0°C and 100°C, the arrows showing the effect of increasing temperature (data is indicative only but based on [64, 135]; exact data is plotted below) or increasing water activity. The wavelength range 0.01 - 100 cm is equivalent to 3 THz - 0.3 GHz respectively. As the temperature increases, the strength and extent of the hydrogen bonding both decrease. This (1) lowers both the static and optical dielectric permittivities, (2) lessens the difficulty for the movement dipole and so allows the water molecule to oscillate at higher frequencies, and (3) reduces the drag to the rotation of the water molecules, so reducing the friction and hence the dielectric loss. Note that ε∞ (i.e. the dielectric permittivity at short wavelengths) does not change significantly with temperature. Most of the dielectric loss is within the microwave range of electromagnetic radiation (~1 - ~300 GHz, with wavenumber 0.033 cm-1 - 10 cm-1, and wavelength 0.3 m - 1.0 mm respectively). The frequency for maximum dielectric loss lies higher than the 2.45 GHz (wavenumber 0.0817 cm-1, wavelength 12.24 cm) produced by most microwave ovens. This is so that the radiation is not totally adsorbed by the first layer of water it encounters and may penetrate further into the foodstuff, heating it more evenly; unabsorbed radiation passing through is mostly reflected back, due to the design of the microwave oven, and absorbed on later passes. The above data can also be plotted using a Cole-Cole plot, as opposite, of the dielectric permittivity versus the dielectric loss. The red circular arcs show the effects of temperature varied by 20°C amounts from O°C to 100°C, whereas the blue lines shows the variation with temperature at fixed wavelengths (1.3 - 201 GHz). 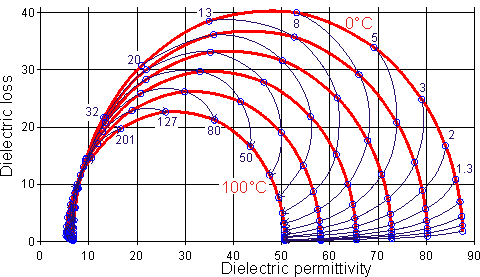Note that the shifts in the dielectric properties with temperature gives rise to maxima in the temperature behavior at constant frequency. Plotted opposite are equations derived for pure water over the range for -20°C ~ +40°C [683], extrapolated (dashed lines) to indicate trends. The equations that generate these curves involve 15 optimized parameters. Further data has been published [1185]. The temperature effect on the dielectric relaxation time is shown on another page.

The dielectric loss factor (Lf) increases to a maximum at the critical frequency.

Dissolved salt depresses the dielectric constant dependent on its concentration (C ) and the average hydration number of the individual ions (H_N)

Figure 2. Dielectric and dielectric loss of a dilute salt solution between 0°C and 100°C (dashed lines; the solid lines shows the pure water curves as Figure 1 above), the arrows showing the effect of increasing temperature. Data is indicative only; exact data is plotted below. The salt decreases the natural structuring of the water so reducing the static dielectric permittivity, in a similar manner to increased temperature. At the lower frequencies the ions are able to respond and move with the changing potential so producing frictional heat and increasing the loss factor (Lf). Thus whereas water becomes a poorer microwave absorber with rising temperature, a lossy salty food such as salt meat becomes a better microwave absorber with rising temperature. The rate that the temperature of such lossy salty food rises on microwaving increases as it is proportional to this increasing loss factor and inversely proportional to the density times specific heat (which change less with temperature); i.e. the hotter it gets, the quicker it gets hotter.  Plotted opposite are equations derived at 10 parts per thousand w/w (ppt) salinity for the range for -20°C ~ +40°C [683], extrapolated (dashed lines) to indicate trends. Further recent data is available [1074]. Plotted opposite are equations derived at 2.45 GHz (typical microwave oven frequency) for different parts per thousand w/w (ppt) salinity for the range for -20°C ~ +40°C [683], extrapolated (dashed lines) to indicate trends. The equations that generate these curves involve 46 optimized parameters.

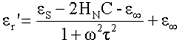
The dielectric loss is increased by a factor that depends on the conductivity (Λ, S cm² mol^-1; S = siemens = mho), concentration and frequency. It increases with rise in temperature and decreasing frequency.

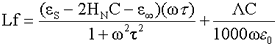
Ensuring that all units are SI, the 1000 factor in the denominator goes. This 1000 is a conversion between SI and cm, mol, L units. This emphasises that careful consideration must be given to the units used in the microwave literature.

Bound water and ice have critical frequencies (λ_S) at about 10 MHz (τ about 0.1 μ) with raised static dielectric permittivities (ε_S). At the much higher frequency of microwave ovens such water has a low dielectric permittivity (e.g. ice-1h, ε_∞ = 3.1; cf. ice-1h, ε_S = 97.5 [94];  ε_S water (0°C) = 87.9), and is almost transparent, absorbing little energy. This is particularly noticed on thawing where the thawed material may get very hot whilst unthawed material stays frozen. Therefore for balanced heating the thermal effects must be evenly distributed, i.e. there should not be pockets of salty water within a poorly conducting matrix.

The electromagnetic penetration is infinite in a perfectly transparent substance and zero in reflective material (e.g. metals). At the microwave oven frequency (2.45 GHz), most energy is absorbed by water. The attenuation (α) is given by:

As

if tanδ is « 1

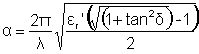
This equation may be approximated where the attenuation is (approximately) directly proportional to the loss factor and inversely proportional to the wavelength times the square root of the relative dielectric constant:

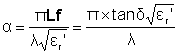
For a plane wave, incident microwaves decrease to 1/e (0.36788; i.e. 63% absorbed) in a penetration distance Dp given approximately by::

At 2.45 GHz:

Thus, using water at 25°C, ε_r´ = 78. Lf =12, tanδ = 0.15 and Dp = 1.4 cm but the effect is much greater in supercooled water (that may be present in frozen food) where at -17.78°C (i.e. 0°F), ε_r´ = 74.4. Lf =40.1, tanδ = 0.54 and Dp = 0.43 cm [1074].

The amount of power (P, in watts m^-3) that is absorbed is given by:

P = 2πfε₀LfE²

where ε₀ = 8.854x10^-12 F m^-1, f is the frequency (Hz, = ω/2π) and E is the potential gradient (V m^-1).

^a Background theory and definitions are given on another page, as is dielectric spectroscopy. [Top]

^b Hydroxyl groups in sugars and polysaccharides behave similarly, creating a high shear environment. Fats exhibit a lesser effect but their lower specific heat gives rise to rapid heating. [Back]

^c Note the relaxation time is the reciprocal of the frequency in radians per second whereas the electromagnetic frequency is commonly reported in cycles per second (Hz). [Back]

^d The change of static permittivity with temperature (-35°C < t < 100°C) may be approximated by the equation ε_S(t)=A.e^-bt where A= 87.85306 and b=0.00456992 [588]. [Back]