|
Professor: Dr. Nathan Louis Gibson
Office: Zoom
Office Hours: TBDCourse Website:https://sites.science.oregonstate.edu/~gibsonn/Teaching/MTH656-001S21 |

|
Measurable Student Learning Outcomes: A successful student in MTH 656/659 will be able to:
Course Description
Background:
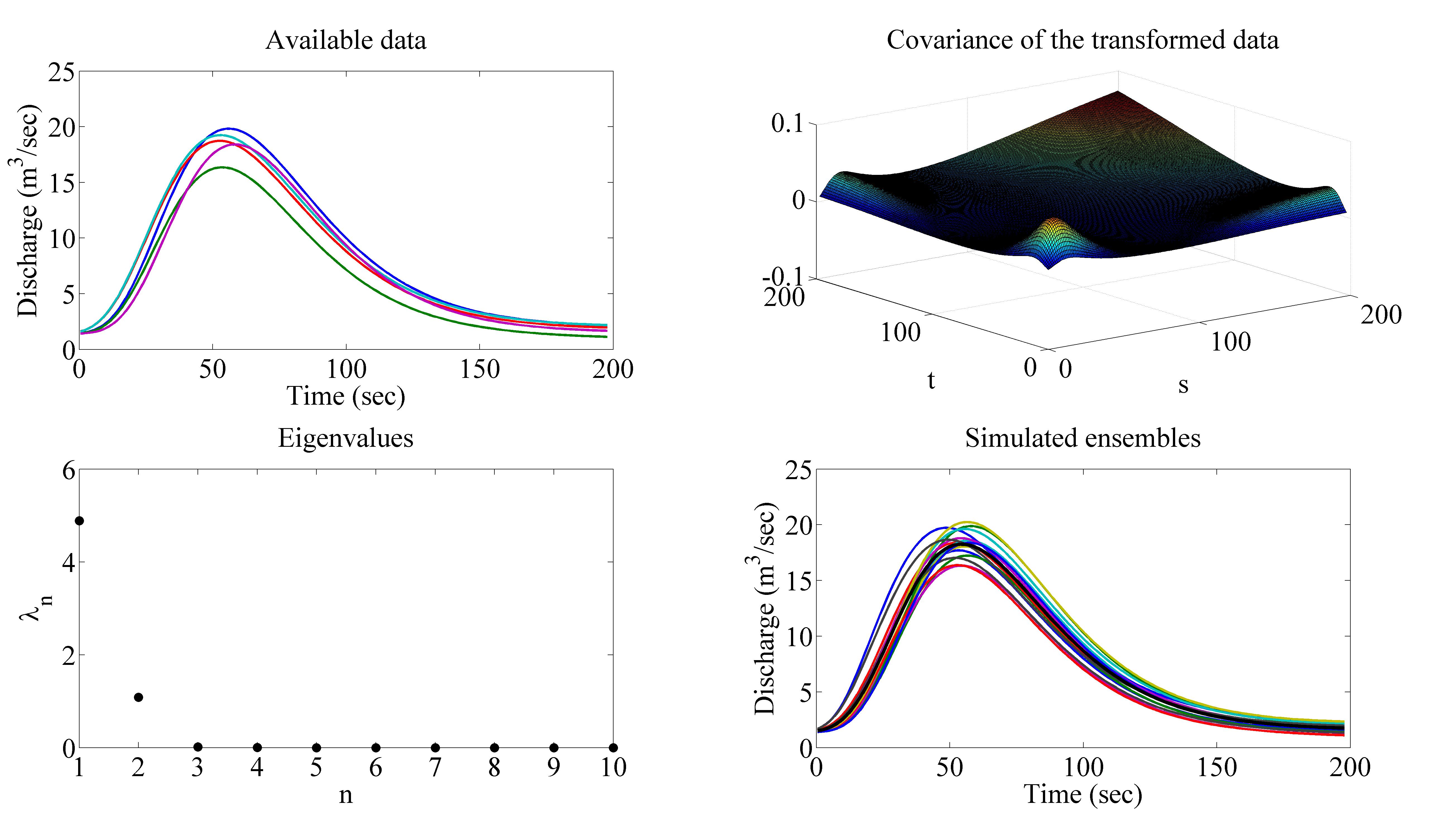
Accurate estimates for the propagation of uncertainty through complex systems is necessary for predictive simulation, robust design, and failure analysis. This course is primarily concerned with the numerical solution of differential equations which include uncertainty, either in system parameters, source terms, or in initial/boundary conditions. 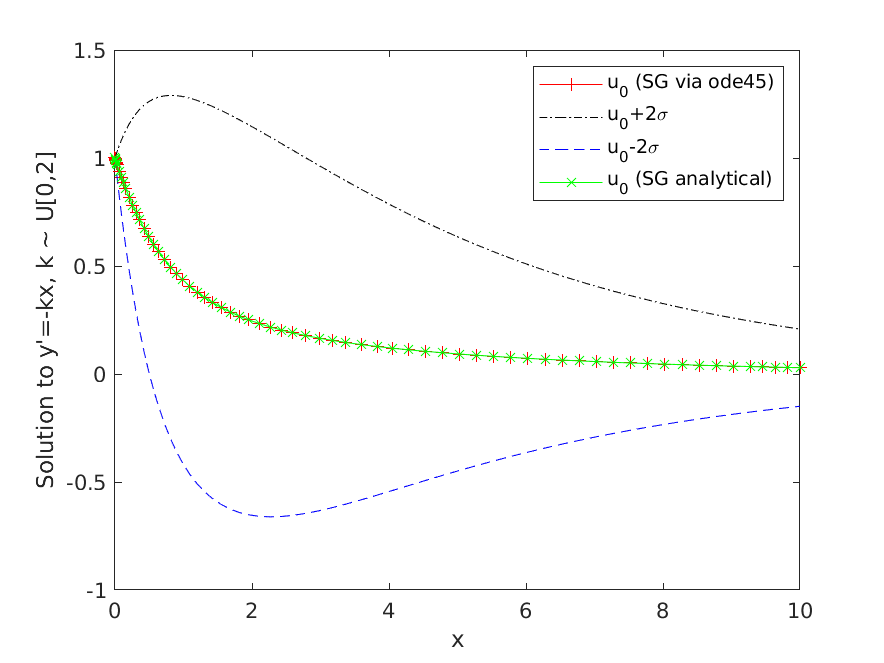
Fig: Stochastic Galerkin approximation for a Random ODEContent:
In this course we will develop basic mathematical foundations and algorithmic aspects of stochastic computations and uncertainty quantification theory.
The necessary background in polynomial approximation, numerical integration, and probability theory will be developed.
While the emphasis will be on random differential equations, stochastic differential equations will also be discussed.
Methods covered will include Karhunen–Loève expansion, Stochastic Galerkin including generalized Polynomial Chaos, Stochastic Collocation including Smolyak sparse grids, Spectral Stochastic Finite Element Method, Euler-Maruyama method for SDEs, among others.
Topics will include convergence, stability, error estimates and implementation issues.
As time allows, we will discuss challenges arising from high-dimensional problems, inverse problems/robust optimization and data assimilation.
The course will provide a working understanding of several numerical solution methods as well as MATLAB sample codes for examples of applications.
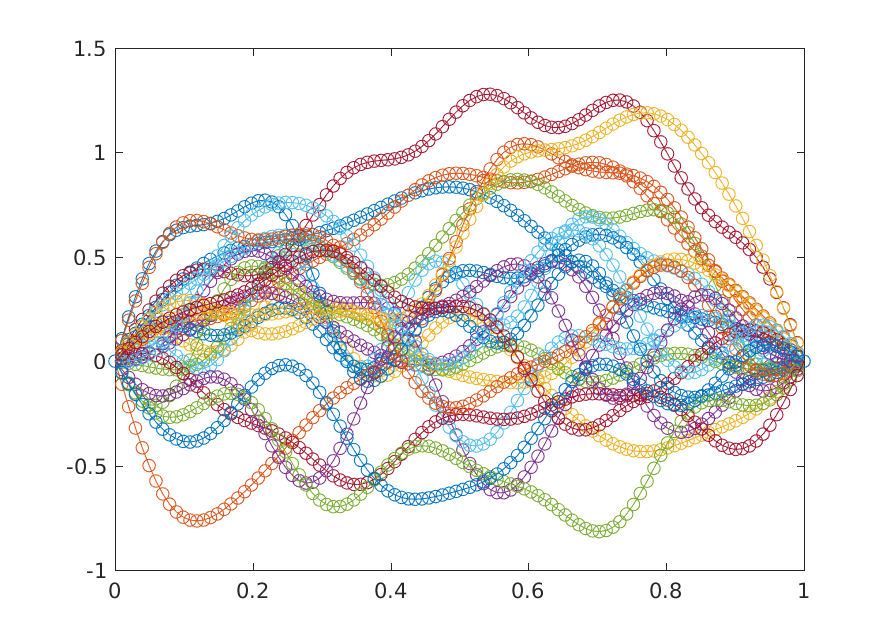
Fig: Karhunen–Loève expansion approximation to a Brownian Bridge
Learning Outcomes:
The course is intended for graduate students of mathematics, computer science, statistics, and other science and engineering disciplines. The content of the course is largely self-contained. For general
pre-requisites, students should have some familiarity with probability, linear algebra, ordinary and partial differential equations, and introductory numerical analysis. Please contact the instructor with questions about background.
Text:
There is no required text for the course, but the following are recommended (in order of importance):
| Homework | 50% |
| Final Project | 50% |
| Total | 100% |
A computational/mathematical project is required for this course. Students must work
individually on a topic/problem of their choice involving random or stochastic problems
(can be from research/thesis work). Students must submit a typed (less
than or equal to two pages) research proposal, including questions to be
answered midway through the course.
Final papers will be submitted as a typed report, including tables or
graphs as figures with captions and references to these inside the
body of the text, and a bibliography with at least two external sources.
Each student will give brief (10 minute) presentation on their results during the last day of classes or the
day reserved for a final exam.
Oregon State University has subscribed to a Total Academic Headcount (TAH) Site License for MATLAB. This new licensing includes many, but not all MATLAB toolboxes. OSU faculty, staff and students can install on up to 4 personally-owned devices or computers.
For more information visit Information Services -- MATLAB or matlab.mathworks.com.
The following are online resources for learning Matlab:
Homework
Homework is required for this course. There will be a few short
assignments, and they will be posted on the website. Problems will
reinforce theoretical and computational concepts from lecture.
Students are encouraged to
work together, but must turn in individual papers.
Term Project
Matlab
Matlab codes will be provided for homework assigments.
Supplements