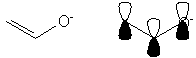
The difference is that the Coulomb and resonance integrals for oxygen and its bonds are different from those defined for carbon. Thus when we set up the secular determinant, the specific terms will vary somewhat.
A. The system you wish to analyze is analogous to an allyl system:
The difference is that the Coulomb and resonance integrals for oxygen and its bonds are
different from those defined for carbon. Thus when we set up the secular
determinant, the specific terms will vary somewhat.
I will define position 1 as the oxygen. Instead of a-E,
I will substitute the Coulomb integral value for oxygen anf get α+0.2β-E.
For the off-diagonal elements, I will substitute 0.8 β for β. Thus, we get for the secular determinant:
| α+0.2β-E | 0.8 β | 0 |
| 0.8 β | α-E | β |
| 0 | β | α-E |
Divide by β ,substitute the standard definition for x and
collect terms:
| x + 0.2 | 0.8 | 0 |
| 0.8 | x | 1 |
| 0 | 1 | x |
so the secular equation is
x3 + 0.2x2 - 1.64x - 0.2 = 0
Plot this out, and you find roots of x = -1.325, -0.125, 1.245. The energy diagram is thus:
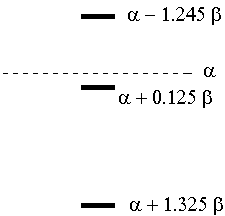
The total resonance energy is the final total π energy minus the energy of the electrons on the isolated atoms. This requires we "assign" electrons as coming from specific atoms, so I will assume one electron from each carbon and two from oxygen.
Initial energy: 2α + 2(α +
0.2β) = 4α + 0.4β
Final energy: 2(α + 0.125β) +
2(α + 1.325β) = 4α
+ 2.9β
Resonance energy = 2.5β
Compare this to the resonance energy of the double bond (2β) and it becomes clear that there is a substantial interaction. (Alternative comparisons are OK: the allyl anion, for example). An interesting sidelight is to observe that the HOMO is actually higher in energy than one would expect for an alkoxide, but that the net resonance energy is tied up in the lowest energy orbital. Further, if you wish, you can examine the reactivity of oxygen versus carbon by looking at coefficients on the two terminal atoms.
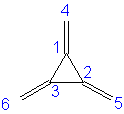
B. The four secular determinants are:
| x | 1 | 1 | 1 | 0 | 0 | ||
| 1 | x | 1 | 0 | 1 | 0 | ||
 |
1 | 1 | x | 0 | 0 | 1 | |
| 1 | 0 | 0 | x | 0 | 0 | ||
| 0 | 1 | 0 | 0 | x | 0 | ||
| 0 | 0 | 1 | 0 | 0 | x | ||
| x | 1 | 0 | 0 | 1 | 1 | ||
| 1 | x | 1 | 0 | 0 | 0 | ||
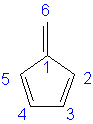 |
0 | 1 | x | 1 | 0 | 0 | |
| 0 | 0 | 1 | x | 1 | 0 | ||
| 1 | 0 | 0 | 1 | x | 0 | ||
| 1 | 0 | 0 | 0 | 0 | x | ||
| x | 1 | 0 | 1 | 1 | 0 | ||
| 1 | x | 1 | 0 | 0 | 1 | ||
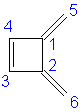 |
0 | 1 | x | 1 | 0 | 0 | |
| 1 | 0 | 1 | x | 0 | 0 | ||
| 1 | 0 | 0 | 0 | x | 0 | ||
| 0 | 1 | 0 | 0 | 0 | x | ||
| x | 1 | 0 | 1 | 1 | 0 | ||
| 1 | x | 1 | 0 | 0 | 0 | ||
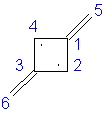 |
0 | 1 | x | 1 | 0 | 1 | |
| 1 | 0 | 1 | x | 0 | 0 | ||
| 1 | 0 | 0 | 0 | x | 0 | ||
| 0 | 0 | 1 | 0 | 0 | x | ||
These obviously lead to different secular equations and thus the observed roots.
1. From the given roots, remember that the negative roots lead to the bonding orbitals. All of these have some resonance stabilization versus 3 isolated double bonds (E = 6α + 6β); none are as stable as benzene (E = 6α + 8β).
Trimethylenecyclopropane: 6α + 7.301β
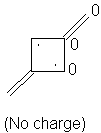
Methylenecyclopentadiene: 6α + 7.466β
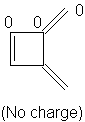
1,2-Dimethylenecyclobutene: 6α + 7.208β
1,3-Dimethylenecyclobutanediyl: 6α + 6.472β
2. Recalling that the charge is given by
q = 1 - Σnici for all
occupied orbitals, we find the following charges:
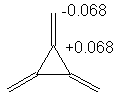 |
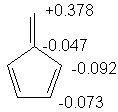 |
 |
 |
Note: there was an error in the coefficients for Ψ3 in 1,3-dimethylenecyclobutanediyl. If your answer based on this data was incorrect, you will still receive fill credit.
3, 4. We really have to discard the 1,3-dimethylenecyclobutane from consideration; this is predicted to be a ground state radical and thus it has separate reactivity. This is clearly the most reactive molecule of the four.
That being said, methylenecyclopentadiene will be quite reactive to nucleophiles: it has a low energy LUMO, and this LUMO is localized on one atom. The next lowest LUMO is for trimethylenecyclopropane.
The highest HOMO is in 1,2-dimethylenecyclobutene; the other two have identical energies for the HOMO. The trimethylenecyclopropane may be a bit more reactive because of the orbital degeneracy; HOMO-1 is lower for methylenecyclopentadiene.