You are here: start » whitepapers » sequences » qmoperatorseq
Quantum Operators
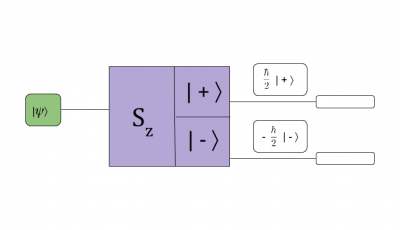
Spin 1/2 systems are the simplest quantum systems and the Stern-Gerlach experiment is at the heart of quantum measurement theory. From our research Making sense of quantum operators, eigenstates, and quantum measurements, we found that many of our students share the common misunderstanding that the eigenvalue equations $$S_z \vert \pm \rangle = \pm\frac{\hbar}{2} \vert \pm \rangle$$ is a mathematical description of what happens inside the Stern Gerlach device. Then they assume that the state vectors that come out of the Stern-Gerlach apparatus have the eigenvalues attached to them (as shown in picture below).
This sequence of activities represents our current attempt to stop this misunderstanding, hopefully before it develops. The activities can be divided into two parts. The first part is used to introduce the students to the mathematics behind a quantum mechanical system. The prerequisite for this sequence is linear algebra. The second part is used to build student understanding of the Stern-Gerlach experiment. A simulation of Stern-Gerlach experiments is used to provide a virtual experience for the students.
Activities
Linear Algebra prerequisites to quantum mechanics:
- Linear Transformation Activity (Estimated Time: 10 min for student task, 30 min for class discussion) This small group activity is designed to help students' understanding of the geometry behind linear transformation matrices and introduce the idea that eigenvectors are vectors whose direction is unchanged by the transformation. This activity is a prerequisitie to the Eigenvalues and Eigenvectors Activity.
- Eigenvalues and Eigenvectors Activity (Estimated Time: 15 min for student task, 30 min for class discussion) Student practice finding eigenvalues and eigenvectors. One of the outcomes of this activity is to convey the students that the dimensional information from a matrix is carried by the eigenvalues, not the eigenvectors.
- Projection Operators (Estimated Time: 20 minutes) This activity is designed to introduce students to projection operators. Students are asked to create a projection operator by taking an outer product of a vector with itself. This activity is an important prerequisite to the Spin-1 Interferometer activity.
Stern-Gerlach Simulations
- Spins Intro Activity (Estimated Time: 10-15 minutes) This small group activity is designed to introduce students to the Stern-Gerlach Simulations and to use the simulation to measure probabilities.
- Identifying Unknown States in a Spin-$\frac{1}{2}$ System (Estimated Time: 30 minutes) This activity helps students to think about the relationship between a quantum state and the probabilities of measuring that state to have spin up or down in the $x$, $y$, and $z$ directions. This activity shows that a quantum state by itself is dimensionless. Furthermore, this activity emphasizes the fourth postulate of Quantum Mechanics.
- Spin-1 Interferometer (Estimated Time: 30 minutes) This small group activity helps student to practice using projection operators in a spin-1 system to find the state resulting from the combination of several Stern-Gerlach output beams. This activity is designed to enhance students understanding of the allegory of Stern-Gerlach experiment.