Time Evolution of Harmonic Oscillator States

Highlights of the activity

1. Students use Maple to animate wavefunctions consisting of linear combinations of eigenstates.
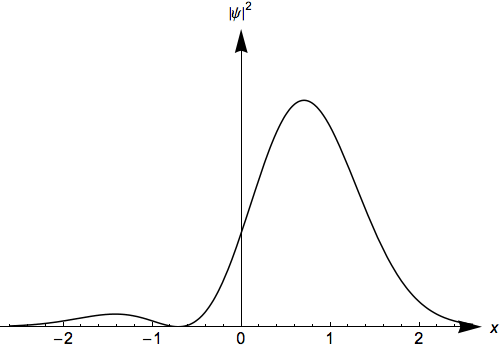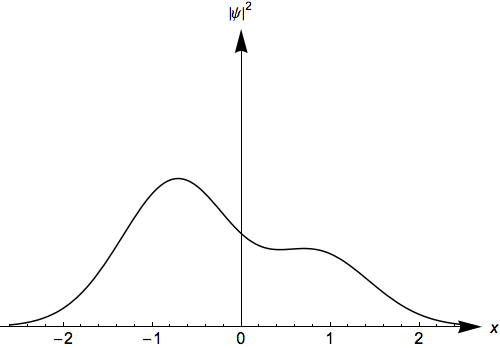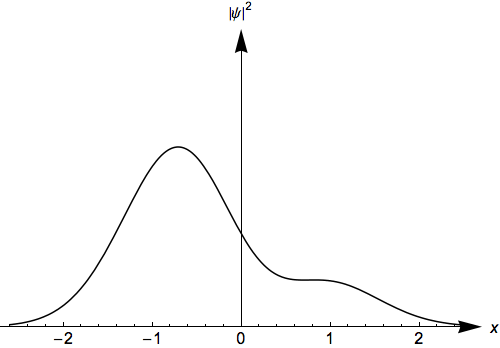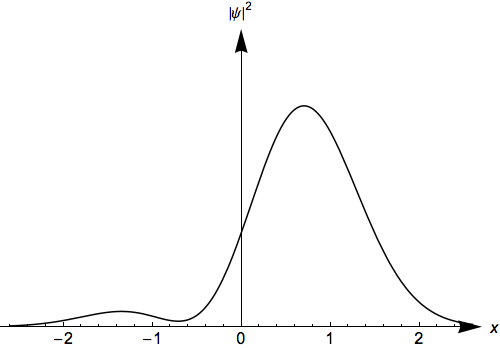
2. Students see that single eigenstates are stationary states
3. Students see that linear combinations of energy eigenstates are states that change with time

Reasons to spend class time on the activity

Time evolution is an a major topic in most quantum mechanics courses. Students often have difficulty understanding what makes some states stationary and other states evolve with time. Students often have difficulty transforming solutions to the time-independent Schrödinger equation into time dependent solutions. This activity was designed for students to construct a solution to the time-dependent Schrödinger equation and then observe the state's time evolution. This activity is the same as the infinite well activity: Time Evolution of Infinite Well Solutions

Reflections

• Reflections from the original implementation.

• Reflections from "official" adapters/adopters.

• Reflections from the general public.

Instructor's Guide

• Wiki version