You are here: start » activities » main
9 Atomic Wells
Highlights of the activity
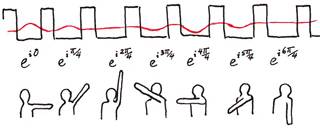
- Nine students are selected from the class to represent the wave function of an atom, where the wave function is represented by $$\sum_{n=1}^{N} A\, e^{ikna}\; \phi (x-na) \; \; ,$$ $$k=\frac{-N\pi}{L}, … ,\frac{-2\pi}{L},0, \frac{2\pi}{L}, \frac{4\pi}{L}, … , \frac{N\pi}{L} \; \; .$$
- Each student will then put their arm in a particular direction to represent the value of their $e^{ika}$ term.
- The class is then asked to determine the wave vector of the envelope function.
- A second group can be selected to perform the same demonstration with a different wave vector.
- The energies of the eigenstates can then be compared using $$E=\alpha + 2\beta \, \cos{ka} \; \; .$$
Reasons to spend class time on the activity
Students will oftentimes have a difficult time realizing that, given the spacing of the potential wells and the number of potential wells in the system, they can formulate the eigenstates of an electron in a potential landscape with little challenging computation. This exercise is designed to help students practice looking at the graphical representation of an eigenstate and determining the wave vector of the eigenstate.