You are here: start » whitepapers » narratives » intro
Example of the First "Name that Experiment" Wrap-Up Discussion
Physics Paradigms Interlude
Tuesday, April 26, 2011 (Day 2)
This narrative presents an example of an instructor engaging students in thinking conceptually about the partial derivatives they encounter in thermodynamic contexts. The instructor, David Roundy, invites students to think about how they would measure the quantities represented by a partial derivative. During this class session, Day 2 of the thermodynamics paradigm, he introduces this “Name the Experiment” process by engaging the small groups in designing thought experiments for a variety of thermodynamic partial derivatives. The narrative$^{1}$ below interprets the wrap-up discussion that follows this small group activity.
A partial derivative such as $$\left(\frac{\partial A}{\partial B}\right)_{C}$$ represents how much a quantity $A$ changes as the quantity $B$ changes when the quantity $C$ is held constant. David wants the students to be able to look at the symbols stating a partial derivative and to envision an experimental process that it represents. In particular, he wants them to realize that the quantity $C$ is something that must be held constant experimentally when measuring how the quantities within the parentheses change.
During Day 1 of the thermodynamics paradigm, David introduced the concept of thermodynamic state variables as well as operational definitions for the various state functions. The students did an experiment in which they measured the heat capacity of water and the latent heat of fusion of ice. David introduced the thermodynamic definition of entropy:
$$\Delta S = \int \frac{\text{đ}Q}{T}$$
and instructed the students, in the analysis of their experiment, to find the entropy change as ice was melted and water heated by integrating the measured heat.
On Day 2, David introduced the First and Second Laws of Thermodynamics. He explained entropy as “the thing that can increase, but not decrease.” He mentioned reversible processes briefly and explained how a reversible process must have zero entropy. As an example, he explained how dunking a hot metal cube into water is an irreversible process. He also talked about slow processes and fast processes, that slow processes are more likely to be reversible than fast. He listed many types of processes including quasistatic (“a process slow enough that the system is effectively in thermal equilibrium the entire time”), reversible, irreversible, adiabatic (“a process in which heat is not exchanged with the environment”), spontaneous, fast, and slow. Then he used the theoretical model of a piston to talk about work, the First Law of Thermodynamics (“conservation of energy”) and the thermodynamic identity $$dU = TdS – pdV$$ as a result of the First Law, combined with the definitions of work and entropy), which is a consequence of the First Law.
Starting the Small Group "Name the Experiment Activity" [00:30:44.09]
At this point in the session, David shifted to small group work. He gave each of the group a thermodynamic derivative and told them they needed to design an experiment that would measure the derivative. The derivatives were
\begin{equation} \ \left(\frac{\partial T}{\partial V}\right)_{S}, \left(\frac{\partial V}{\partial p}\right)_{T}, \left(\frac{\partial L}{\partial \tau}\right)_{T},\left(\frac{\partial U}{\partial T}\right)_{V}\end{equation} \begin{equation} \ \left(\frac{\partial V}{\partial T}\right)_{p},\left(\frac{\partial L}{\partial T}\right)_{t}\,\left(\frac{\partial V}{\partial p}\right)_{S},\left(\frac{\partial L}{\partial t}\right)_{T},\left(\frac{\partial U}{\partial p}\right)_{S}\end{equation}
where $T$ represents temperature; $V$, volume; $p$, pressure; $L$, length; $\tau$, tension; $U$, internal energy; and $S$, entropy.
The last derivative of equation $(2)$ is the most challenging, but the rest are semi-randomly ordered so as to not give a hint as to how they are related. Groups that finished early were asked to try the last, and most challenging, problem. The first, third, and last derivatives of equation $(1)$, and the first, third, and last derivatives of equation $(2)$ $%Derivatives #1, 3, 4, 5, 7 and 9%$ require that the standard thermodynamic variables, pressure, and volume have been introduced. The third derivative of $(1)$ and second derivative of (2) $%Numbers 3 and 6%$ require that students be able to apply thermodynamic concepts to 1-D systems, such as strings or rubber bands. The last derivative of $(1)$ requires students to have a working knowledge of the First Law, while the last derivative of $(2)$ requires students to recognize how to perform an adiabatic measurement, and how that relates to entropy.
As David and his teaching assistant circulated among the small groups, they looked over what was on the white boards and listened to what the members of a small group were saying to see whether the group was paying attention to what was to be held constant. If not, David and the TA intervened with questions, such as “how do you keep the temperature fixed?” to nudge the group toward recognizing this critical aspect of the task. In addition, they asked groups how they would make measurements, so as to reinforce the lessons of the previous day regarding operational definitions of thermodynamic quantities.
David gave another more challenging partial derivative to groups who had finished before he thought the whole group was ready for the wrap-up discussion.
After the groups were given time to work, David brought the class back together and asked the students to share what they done. As the groups presented, he gave advice about the different scenarios.
Starting the Wrap-Up Discussion: First Group's Presentation
After about fifteen minutes, David began the wrap-up discussion by selecting the group who did the first partial derivative.
${\bf [00:46:58.22]}$
${\bf Roundy}:$ So, let's just very quickly, if we could start with you, we'll just go around, and you can tell us what the derivative was and how it's measured in one minute or less.
David has the groups report out in the same order as he gave out the derivatives. Although the first was an easy one, he tries to avoid going in an easiest-to-hardest order. This insures that the discussion gets beyond the easiest ones if there is a small number of groups or time is limited.
${\bf [00:47:15.03]}$
The first group had worked on the partial derivative of the change in temperature with a change in volume, holding the entropy fixed, $\left(\frac{\partial T}{\partial V}\right)_{S}$ .
A student held up his small group’s whiteboard, which showed a piston with insulated walls and a thermometer inside, on the left side of the white board. They had understood that holding entropy constant means isolating the system so that no energy is lost or gained. (They had also started working on another partial derivative on the right side of the white board.)
${\bf \text{Student 1}}:$ So ours was $dT$ d(volume) holding $S$ constant $\left[\left(\frac{\partial T}{\partial V}\right)_{S}\right]$ basically we derived kind of a complex system here. Thermally insulated, thermometer in there, so basically we can change the volume inside, measuring the volume of air or some gas in there.
${\bf [00:47:36.23]}$
${\bf Roundy}:$ Ok.
While watching the video, David commented that an expert response would be similar, to use an insulated piston and change the volume while measuring the change in temperature inside.
Second Group's Presentation
The second group had worked on the partial derivative of volume with respect to pressure, holding the temperature constant, $\left(\frac{\partial V}{\partial p}\right)_{T}$ .
They also had drawn a piston, but with thin walls. A arrow pointing down represented a force pushing on the piston. By writing “very slowly” next to the F representing a Force, they indicated that they had understood this process needed to happen slow enough for any heat generated to dissipate through the walls of the piston. To the left of the piston, they had written “area constant” and to the right, “measure height.” These indicate that they understood that the volume would be the product of the area and height and would change as the height changed. Underneath the piston, they had written “Surroundings at constant temperature; system not insulated” indicating that they understood that the piston needed to be in an environment with constant temperature and that any heat generated in pushing the piston down slowly would be dissipated through the thin walls.
${\bf [00:47:49.12]}$
${\bf \text{Student 2}:}$ So we're two and uh we change the volume and pressure and keep the temperature constant. So if we had a cylinder with some gas in it and we allowed heat transfer to go out of the wall, uh, it wasn’t insulated it would come to equilibrium with the outside so it would keep the temperature also reversible.
${\bf [00:48:11.14]}$
${\bf \text{Student 3}:}$ Varying the force applied across constant area and measuring how the volume changed.
While watching the video, David commented that this was another easy experiment. They did not have a mechanism for picking a temperature rather than room temperature but they did explicitly discuss how to keep the temperature fixed. An expert response would be very similar, a piston with weights perhaps on top and thin metallic walls that conduct heat well. He would change the weight and measure the change in volume, being sure to wait a long time for thermal equilibrium, at room temperature, and one could adjust that with a thermostat or put the whole device in a refrigerator or mountain stream.
Third Group's Presentation
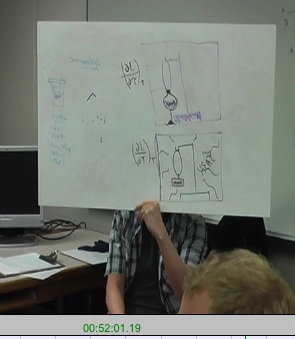
The third group had worked on the derivative of length with respect to tension at fixed temperature, $\left(\frac{\partial L}{\partial \tau}\right)_{T}$.
They showed a complex drawing with two pistons, a rope, mass on a pulley, and a cooling system (fan).
${\bf[00:48:20.05]}$
${\bf \text{Student 4}:}$ OK, yeah so we have change in length due to the change in tension. So we had two pistons, one with a rope and then a mass on the pulley on one of them, so you can change the tension by adding masses to this side. And then our cooling system (moves hand around circle of enclosure) because when you change the tension on the string, the temperature of the string will increase, so you have to change the cooling system to keep the temperature the same, so that’s our system basically. ${\bf[00:49:01.05]}$
While watching the video, David commented that his “expert” solution would probably be a bit simpler: hang a weight from a rubber band, and measure its length. Then add a bit more weight, and wait long enough for it to equilibrate at room temperature. As before, one could use a thermostat or a walk-in-freezer to do the experiment at different temperatures. This example was similar to the rubber band lab that the students would do later in class, probably in the next week.
David noted that this solution was interesting because they included a pulley system. They were changing the tension on the rope by changing the weight on the pulley.
Corinne commented that students had to actually think about how they would construct an experimental apparatus rather than defaulting to a piston.
David noted that having problems that all use pistons is boring and for a third experiment why not use pulleys? The students’ mechanism for keeping the temperature fixed was also quite interesting because they employed a fan rather than just saying we'll wait for the temperature to equilibrate. That seems like they were again thinking experimentally, how would they really keep the temperature fixed?
There are choices to be made in terms of which partial derivatives to give to the students. David commented that often he leaves out the one dimensional problems because they feel redundant to him but sometimes he thinks that they add extra complexity and confusion so perhaps he should include them. Here he did.
Fourth Group's Presentation
The fourth group had worked on the partial derivative of the internal energy with respect to temperature at constant volume, $\left(\frac{\partial U}{\partial T}\right)_{V}$.
This group had drawn a container and indicated that it had a constant volume, with a heater underneath, and probe in the middle of the container to measure the temperature. They explained their reasoning in writing: “From the power, we can get the work done by the resistor. This, if inverted will give us a good ratio between the change in energy and the temperature.”
${\bf \text{Student 5}:}$ So, we ended up getting the change in internal energy with respect to the change in temperature, holding V constant.
${\bf [00:49:13.19]}$
So basically this here, after a little bit of help from (drops board) Aack! Internal energy is really hard, it's a hard one to measure. But we found out it's pretty much the same experiment that we did yesterday, so we can find out essentially the total energy that's being put in the system by the resistor or you know, some other heat source and then you can just measure the temperature as the time passes and we can essentially compare the two on a plot.
${\bf Roundy:}$ So one interesting thing on that, just to add, a volume equals constant is a very very very hard thing to do. Devices that measure things with constant volume – the name for that device is called a bomb. Because you need very very strong walls, and if you increase the temperature too much, it will explode. All right, basically. And chemists have this, because it's a worthwhile measurement to make. ${\bf [00:50:20.25]}$
${\bf TA:}$ Nuclear plants in Japan. A few months ago started leaking because of what…walls start cracking
${\bf [00:50:33.22]}$
${\bf Roundy:}$ So we like to not do things at constant volume. So theoretically it's very easy to do things at constant volume, in practice, it's hard. That's it. Next group.
While watching the video, David noted that this is a measurement of the heat capacity of a gas at fixed volume, and would naturally be done with a bomb calorimeter, much as the students describe. He would have a heating element, and measure how much power it outputs in a given time interval (to measure the energy put into the system), and then see how much the temperature of the gas changes, while holding the volume fixed with very strong walls. One would need to wait quite a while for it to equilibrate, which is a challenge in the experiment the students do in class.
David also commented that this partial derivative was interesting for multiple reasons. One was that fixing the volume is hard experimentally, although not hard conceptually. This partial derivative also was interesting because internal energy is not something that can be measured directly. Changes in internal energy can be calculated via the first law as equal to the energy put into the system (by heating) minus the work done by the system. The work done by the system would be $pdV$; $V$ is constant so $dV=0$ and the work done equals zero. Therefore the change in internal energy would be just the energy put into the system.
If David had asked for the same experiment at fixed pressure, he thinks the students would have given an incorrect answer because they would have neglected work. However, this is a nice problem for this first day because they can get it right. If they had been wrong, what he would have asked them would depend upon how they got it wrong. If he had asked this problem at fixed pressure, in which gas in a cylinder with a piston expands when heated, he would have asked how they knew what the change in internal energy was and hint at the first law and then ask about work being done. Students often believe no work is done if they are not actively changing pressure or volume, which is why they typically make the mistake of neglecting the work done by the system. In the case of thinking about the change in internal energy with respect to temperature at constant pressure, the gas is doing the work pushing up the piston as the gas expands when heated.
Corinne commented that the emphasis is on THEY are actively doing the work, not the system. That seems to be a theme behind several of the different extended comments that David had made, where students only keep track of what they as experimentalists change and not changes in the system as a result of other parts of the experiment.
David noted that the student stated that this was the same experiment they had done the day before but that experiment had been at fixed pressure (open to atmospheric pressure) so even here it is possible the student was recognizing that difference and meaning that the heat measurement was the same but he may have fallen into this mistake of thinking the internal energy change was the same.
The students had done a calorimetry experiment the day before so these students were able to give a correct experiment using the first law. The calorimeter is a Styrofoam cup with a lid, and the ice and water are inside it, along with a resistive heater. By measuring current and voltage, the students know how much energy is added to the system by resistive heating, and we hope the Styrofoam is a sufficient insulator that heating from the room is negligible. Students measure the change in temperature of the ice water. Of course, while there is ice (and the system is well mixed) this temperature should not change, which gives us a measure of how much energy is needed to melt the ice. Once the ice is all melted, we measure the temperature as a function of energy added (i.e. time), and find the heat capacity. In the analysis of the lab, David also asks students to calculate the change in entropy from their data, which requires just a bit of math beyond their actual measurements.
With regard to the thought experiment, at constant volume, it is*almost* like what they did, with the difference being that they did not hold volume fixed, but instead held pressure fixed (at atmospheric pressure). They added a bit of energy (at a time) and measured how much the temperature changed, which in a sense is the inverse of the derivative for which they were creating the thought experiment.
Corinne wondered how important it is that the students have done the calorimetry experiment before they do this partial derivative. David responded that for this particular question, it is very important. For many years, he has always done the calorimetry experiment on the first day of the class. He started this because he wanted more experiments and more understanding of heat.
David also commented that sometimes he wants to reduce the number of partial derivatives used, in favor of redundancy, because one never knows what might happen in the different groups. A group might design a different experiment; with an internal energy partial derivative, there might be groups that do not get a reasonable answer so sometimes it is good to have two groups on an internal energy partial derivative as insurance.
Fifth Group's Presentation
The fifth group had worked on the partial derivative of volume with respect to temperature at constant pressure, $\left(\frac{\partial V}{\partial T}\right)_{p}$ . On their whiteboard they had drawn a picture of a cylinder with a piston with a thermometer inside the cylinder. An arrow pointing down, above the piston, was labeled constant pressure.
${\bf [00:50:46.19]}$ ${\bf\text{Student 7}:}$ We did $dV/dT$ holding pressure constant, so we just have a piston system, and I guess it's frictionless when the piston goes up and down. There's a constant pressure on the outside of it and then a thermometer on the inside suspended somehow. We're gonna make all the measurements, and then add a heating element under it to make it hotter, and then measure the new volume to see the relationship.
${\bf Roundy:}$ And how are you going to keep the pressure constant?
${\bf \text{Student 8}:}$ We'll pretend this is a vacuum, and we'll put weights on there. (laughter)
${\bf Roundy:}$ It doesn't need to be a vacuum, but if you want to do any pressure that’s under an atmosphere, you either need to pull up on it or…Ok, sure, you can be next.
While watching the video, David commented he would do this quite similarly to what they did. One would want a piston with weights on top of it, or if in the atmosphere, possibly a pulley setup for weights to pull *up* on it, if want a lower pressure than atmospheric, and one would need to change its temperature (and the temperature of its surroundings) slowly, and measure how the volume changes. One would have to change the temperature of the surroundings so that the piston system could remain in thermal equilibrium, otherwise this could end up with a temperature gradient.
David noted that was an example where the students had not explicitly drawn how they would control the pressure, which is something that he would normally ask about while circulating during the small group work.
Corinne commented that they also seemed to not know how to get less than an atmosphere of pressure without doing it in a vacuum. The suggestion that they have to pull up seems to have not occurred to them and might not occur to a number of students.
David responded that in a thought experiment, he would do the same thing they did (put the piston in a vacuum) because with vacuum around one can very easily compute the pressure and set it to any value one wishes.
Corinne noted that those new to teaching this class need to be alert to the fact that the students might not know what to do in a more realistic situation where they are working at atmospheric pressure. Sometimes students might know how to push but it might not be obvious to them that the opposite of that is pulling on a piston.
David agreed but also commented that he was very happy to hear the students specify a vacuum because a simpler mistake would be to ignore atmospheric pressure and simply divide the applied force (the weight) by the area.
Sixth Group's Presentation
The sixth group had worked on the partial derivative of length with respect to temperature at constant tension, $\left(\frac{\partial L}{\partial T}\right)_{\tau}$.
This group had drawn two versions of a rubber band stretched by a hanging mass, the top diagram for change in length with respect to tension at constant temperature and the bottom diagram for change in length with respect to temperature at constant tension. The bottom diagram included squiggly lines that were labeled HEAT. The students reported on the bottom experiment, with constant tension.
${\bf [00:51:33.05]}$
${\bf\text{Student 8}:}$ Oh yeah, we're going next. So we did number 6, which is change in length, change in temperature, holding tension constant.
${\bf\text{Student 9}:}$ Which was the pretest
${\bf \text{Student 8}:}$ So basically, we had a rubber band and we put a mass on it so we can measure tension and we're not going to change the mass so it's at constant tension. We're gonna place that in some closed area and then increase the temperature, or change the temperature or heat it up…
While watching the video, David commented that he would hold the tension fixed just as these students did, by hanging a weight from the rubber band. However, holding the tension fixed at different temperatures is potentially tricky. Either one needs to adjust the thermostat of the room, or move the experiment to some place with a different temperature. Or use a heat bath as in the experiment done in a later class, submersing the rubber band in water at a varying temperature. This question, like the earlier one dimensional one (#3), is a precursor to the rubber band lab the students do in a later class, which measures tension as a function of both length and temperature.
David noted that they held the tension fixed with a weight and were a little vague but by putting it in a box and changing the temperature of the box they changed its temperature. With temperature one cannot change it quickly and have reasonable results because one will leave thermal equilibrium so changing the temperature ends up looking similar to holding it fixed.
Seventh Group's Presentation
The seventh group had worked on the partial derivative of volume with respect to pressure at constant entropy, $\left(\frac{\partial V}{\partial p}\right)_{S}$.
This group had drawn a piston in an isolated cylinder.
${\bf [00:52:03.04]}$
${\bf Roundy:}$ Next group.
${\bf\text{Student 10}:}$ Ours is like one of the other ones. We just have a piston system here. The actual thing we were testing was $dV/dP$ holding $S$ constant. and so to hold S constant, we just insulated it, and you can change the pressure and volume.
${\bf Roundy:}$ You change the pressure how?
${\bf \text{Student 10}:}$ Uh, by applying force to the piston.
While watching the video, David commented that this one is quite easy. It involves constant entropy, so he would use an insulated piston. To change pressure, he would add or remove weights from the piston, and then measure the volume by measuring the height of the piston.
David noted that these students did not bother explaining how they changed the pressure or how they measured the volume. This might be due to fatigue since they had just spent a lot of time listening to almost the same experiments and it perhaps felt obvious to them at this stage and not worth commenting on.
Corinne commented that he prompted them about how they would control the pressure but not how they would measure the volume. One of the things she has learned over the years is that one can teach the students a lot about what constitutes a complete answer by prompting every single group to give a complete answer until they accept that as a professional norm. There is a tension between that and trying to get through the class before it ends or before one loses the students' attention.
David suggested that prompting them often to make a complete answer is an advantage of switching the dimensionality so that students have different things to say about how they control their system. Keeping their interest, avoiding this fatigue, this boredom, is facilitated by mixing up the dimensionality, sometimes have one dimensional problems with rubber bands as well as the three dimensional problems with pistons.
Corinne noted that when prompting students about the same measurement, they'll often just say “and we'll measure the volume like that other group did.” One can prompt them to say something more and they'll say something very brief, can and do. This cuts down on the boredom but does signal to them that they do have to think about these things when designing an experiment and they must include in a report, to say how they will measure things, not just that they will. She likes to use the reporting out of small group activities as a chance to reinforce or convey those professional norms.
Eighth Group's Presentation
The eighth group had worked on the partial derivative of the internal energy with respect to pressure at constant entropy, $\left(\frac{\partial U}{\partial p}\right)_{S}$.
This group had drawn a picture of a piston in a cylinder and written several mathematical expressions in trying to envision an appropriate process.
${\bf Roundy:}$ And, I don't know if you guys came up with an answer. Can you explain the trouble you had?
${\bf [00:52:40.04]}$
${\bf \text{Student 11}:}$ So we were dealing with $dU/dP$ holding entropy constant. And we didn't really like have the epiphany of how to measure internal energy. That's something we kept kind of having issues with. We really wanted to use this piston somehow. But as we apply more pressure, we thought the temperature would increase, adding heat. And a constraint that we set, for entropy to be held constant, we need that to be zero. So we were trying to find a way that we could change pressure while keeping entropy constant, and it's a weird thing, we tried to do math, and see if we could measure that partial some other way. But we didn't quite finish in time.
${\bf Roundy:}$ Now, many of you, finished yours early and went to another one. Did any of you go to this one? If not, ok. Because this is an interesting one, and it was, in fact, the hardest one.
While watching this video, David commented that he would measure this by using an insulated piston and changing the pressure precisely as he would have in the previous presentation $\left(\left(\frac{\partial V}{\partial p}\right)_{S}\right)$. Once one measures that derivative, one can compute the change in internal energy, which is entirely due to the work done on the system, because $\text{đ}Q=0$, because the entropy is held fixed. So one can invoke the first law [that the change in internal energy is equal to the energy put into the system (in this case $0$) minus the work done by the system], and see that $$\left(\frac{\partial U}{\partial p}\right)_{S} = -p\left(\frac{\partial V}{\partial p}\right)_{S}$$.
David noted that this was a tricky one. It looks like they did not realize that holding entropy fixed meant that there was no heating, no $Q$. They seem to have made the common mistake of recognizing that the temperature will increase and then thinking that entropy will be increasing because it must be being heated.
Corinne wondered if he had let that stand.
David responded that he probably didn’t want to criticize a group that he already felt bad about giving a very hard problem. However, they don't look unhappy in the video and with all the things going on, he might not have actually noticed their mistake of thinking that there was heating going on and that therefore the entropy would change.
David expressed disappointment that he didn't explicitly mention integrating the work, to find the change in internal energy. He had mentioned measuring the change in volume and using the first law and might have pointed at a $pdV$ on the board.
Corinne commented that one way to handle the concern about having given a group a harder example is to acknowledge it, which he had. One can say “this is a harder example” and then ask the question of the class as a whole about the situation rather than focusing on that group further. Say, for example, “the temperature does go up, does the entropy also increase?” and generate that conversation with the class. Another thing to do, when a particular example is hard is tell the students, if your group solves your first example quickly, then go on to this other one (the one that happens to be hard) and that way get the strong groups thinking about the hard example.
David noted that all of the 3-D ones depend upon having already covered the standard thermodynamic quantities, pressure, volume, etc. The internal energy ones require the first law of thermodynamics and an understanding of heat and work and how to measure them, which had been discussed previously during day 1 or the math interlude.
Explicit Articulation of the Purpose of the "Name the Experiment" Activity
After talking about a thought experiment for the last partial derivative, David explicitly discussed why he had the students do what they had just finished doing. Such explicit discussion of one’s teaching strategies can help students see the broader picture of their experiences in learning, particularly in a difficult context such as thermodynamics.
${\bf [00:55:19.20]}$
${\bf Roundy:}$ By the way, the reason I do this Name the Experiment thing, they're going to come back again, later, maybe not tomorrow, but we will have more of this kind of activity using harder derivatives.
He noted that one of the challenging things in thermodynamics is that a problem will be posed and there will be lots of derivatives in the solution and then the lecturer, or the text, will say something like “Oh that’s just isothermal compressibility.”
${\bf [00:56:04.08]}$
${\bf Roundy:}$ Then you say, “it's all beautiful” but “why? why did all that stuff happen?” and the reason all that stuff happened is because you're trying to convert something like that (gestures at final group's derivative) that is hard to measure, or something like this fixed volume thing, where you say, “Fixed volume? That's really hard to measure experimentally” and you might say “I’d like to, right, instead measure” something else easy to measure, and figure out what this thing I'm curious about is.” and so, in order to do that, I'm going to have you work on thinking about how you would actually measure some of these derivatives.
With ten minutes left in the class, David turned to clarifying and extending the concept of heat capacity. The previous day they had done a heat capacity experiment at constant pressure, $C_{p}$ . He contrasted that with heat capacity at constant volume, $C_{v}$. Constant volume means that no work ($pdV$) is being done. From the First Law of Thermodynamics one can say that whatever energy is put into heating, all that energy is going into changing the internal energy so $C_{v}$ is just $dU$ by $dT$ at constant volume. One might think that $C_{p}$ - the heat capacity at constant pressure - would just be $dU$ by $dT$ at constant pressure, but that is not the case. At constant pressure, there is some work being done, so the amount of energy transferred by heating is not equal to the amount of the change in internal energy because there is work being done by the system. Then he discussed a generalized form that could be used in thinking about heat capacity in a variety of cases, including rubber bands.
Notes
$1.$ This interpretative narrative is based upon a video of the class session and discussions with the instructor, David Roundy, the director of the Physics Paradigms Program, Corinne Manogue, and Emily van Zee, a science education researcher. Amanda Abbott transcribed the video. In writing the narrative, Emily drew upon her research in the tradition of ethnography of communication (Hymes, 1972; Philipsen & Coutu, 2004; van Zee & Minstrell, 1997a,b), a discipline that studies cultures through the language phenomena observed. This interpretative narrative presents an example of students growing into participants in the culture of “thinking like a physicist,” in particular in using the ‘language’ of partial derivatives.
References
Hymes, D. (1972). Models for the interaction of language and social life. In J. Gumperz & D. Hymes (Eds.), Directions in sociolinguistics: The ethnography of communication (pp. 35-71). New York: Holt, Rinehart & Winston.
Philipsen, G. & Coutu, L. (2004). The Ethnography of Speaking. In K. L. Fitch & R. E. Sanders (Eds.), Handbook of language and social interaction (pp.l 355-380. Mahwah, NJ: Lawrence Erlbaum.
van Zee, E. H. & Minstrell, J. (1997a). Reflective discourse: Developing shared understandings in a high school physics classroom. International Journal of Science Education, 19, 209-228.
van Zee, E. H. & Minstrell, J. (1997b). Using questioning to guide student thinking. The Journal of the Learning Sciences, 6, 229-271.