You are here: start » courses » prereq » eepre » eeprebbthermo
Prerequisites for Black Body Thermodynamics
Before entering this lesson, students should:
- Have experience with electromagnetic radiation and know what it is.
- Know what a black body object is.
- Have a solid understanding of the first and second thermodynamic laws.
Lecture notes from Dr. Roundy's 2014 course website:
Let's consider the following system. Here we've got two objects in an insulated environment, surrounded by vacuum, so the only way they can exchange energy is through electromagnetic radiation. Further, let's assume that each object is perfectly black, so that it absorbs any radiation incident on it. We will define $Q_1$ and $Q_2$ to be the energy radiated by objects 1 and 2 respectively during a given (short) period of time. We'll assume any energy radiated by one object is absorbed by the other. Also, assume that these objects are large enough that their temperatures are not changing much. 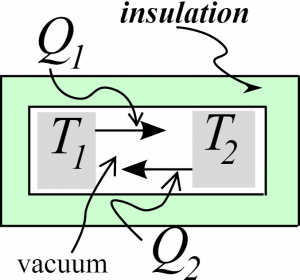
Differing temperatures
First, let us suppose $T_1>T_2$. What can we say about $Q_1$ and $Q_2$ on the basis of the Second Law? $$\Delta S_1 = \frac{Q_2 - Q_1}{T_1} \qquad\qquad \Delta S_2 = \frac{Q_1 - Q_2}{T_2}$$ The second law tells us that $$\Delta S_1 + \Delta S_2 \ge 0$$ $$\frac{Q_2 - Q_1}{T_1} + \frac{Q_1 - Q_2}{T_2} \ge 0$$ $$(Q_2 - Q_1)\left(\frac1{T_1} - \frac1{T_2}\right) \ge 0$$ $$Q_2 - Q_1 \le 0$$ $$Q_2 \le Q_1$$ Equal temperatures
Now suppose $T_1=T_2$, what can we say about $Q_1$ and $Q_2$? They must be the same. It's a little tricky to understand this, since when the two temperatures are the same, the combined change in entropy of the two systems is zero, even if $Q_1≠Q_2$. However, you can easily see that if $Q_1≠Q_2$, then soon the two temperatures would not be the same, and then the heat would be flowing the wrong way.
A grey body
Finally, let us suppose that we replace the right-hand object with one that only absorbs two thirds of incident radiation and reflects the other one third. How much will such a body radiate? We can answer this question by considering the two systems at equal temperatures. We know that two systems at equal temperatures cannot have a heat one another up. The amount radiated by the left-hand body cannot be changed by the change in the right-hand object. However, $1/3$ of that energy will be reflected back and reabsorbed by the left-hand object. Since anything radiated by the right-hand object must also be absorbed by the left-hand object, we conclude that it must only radiate $2/3$ what it would have radiated were it truly black. This tells us that if a body is a poor absorbed of radiation (i.e. is light-colored) it will also be a poor thermal emitter of radiation. Interestingly, our results must hold even if we put a filter that reflects all but one frequency in between the two objects (you do need to convince yourself that such a filter is possible), which means that at every frequency, the absorption must be proportional to the emission, with the same proportionality
Efficiency of solar power $$\eta_\text{max} = 1 - \frac{T_C}{T_H}$$ $$= 1 - \frac{300\text{K}}{6000\text{K}}$$ $$= 95\%$$ For photovoltaic cells, this is not an important limitation (because we can't even approach it due to practical issues).