You are here: start » courses » order20 » vforder20 » vfdivergence
Divergence
Prerequisites
- Limit definition of derivative.
- Understanding of derivative as a ratio of small changes.
- Ability to compute partial derivatives.
- Reading: GVC § Divergence Theorem
- Reading: GVC § Differential Form of Gauss's Law–Electric Field Lines
In-class Content
- Derivation of the Divergence Theorem (lecture - 15 min). We follow “div, grad, curl and all that”, by Schey. The Divergence theorem is almost a lemma based on the definition of divergence. Draw a diagram of an arbitrary volume divided into lots of little cubes. Calculate the sum of all the fluxes out of all the little cubes (isn't this a strange sum to consider!!) and argue that the flux out of one cube is the flux into the adjacent cube unless the cube is on the boundary.
- Visualizing Divergence (Maple Visualization - 30 min) Students practice estimating divergence from graphs of various vector fields. We do this with printouts in dry-erasable sleeves now, with computer follow-up.
- Differential Form of Gauss's Law: Maxwell's Eq 1 & 3: $\Vec{\nabla} \cdot \Vec{E} = {\rho \over \epsilon_0}$, $\Vec{\nabla } \cdot \Vec{B} = 0$ (lecture - 15 min)
Optional In-class Content
- (optional) Divergence of a Coulomb field (requires delta functions) (lecture)
- (optional) Electric field lines (lecture)
Homework for Static Fields
- (DivergencePractice) Calculate the divergence for several made-up functions using rectangular and curvilinear coordinates.
Calculate the divergence of each of the following vector fields. You may look up the formulas for divergence in curvilinear coordinates.
$\FF=z^2\,\hat{x} + x^2 \,\hat{y} -y^2 \,\hat{z}$
$\GG = e^{-x} \,\hat{x} + e^{-y} \,\hat{y} +e^{-z} \,\hat{z}$
$\HH = yz\,\hat{x} + zx\,\hat{y} + xy\,\hat{z}$
$\II = x^2\,\hat{x} + z^2\,\hat{y} + y^2\,\hat{z}$
$\JJ = xy\,\hat{x} + xz\,\hat{y} + yz\,\hat{z}$
$\KK = s^2\,\hat{s}$
$\LL = r^3\,\hat{\phi}$
$\MM = r^3 \cos{\phi}\,\hat{r} + \frac{1}{r^2} \sin^2{\theta}\,\hat{\phi}$
- (DivergencePrism) Verify the Divergence Theorem on a prism.
Consider the vector field $\Vec F=(x+2)\hat{x} +(z+2)\hat{z}$.
Calculate the divergence of $\Vec F$.
In which direction does the vector field $\Vec F$ point on the plane $z=x$? What is the value of $\Vec F\cdot \hat n$ on this plane where $\hat n$ is the unit normal to the plane?
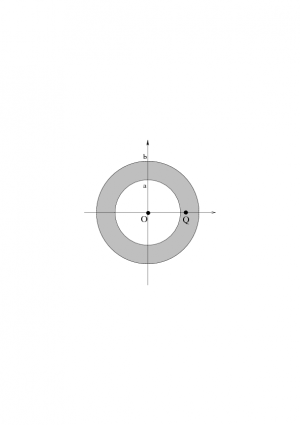
- (DivergenceSpherical) Verify divergence theorem for a spherical shell of matter, starting with an expression for the gravitational field.
The gravitational field due to a spherical shell of matter (or equivalently, the electric field due to a spherical shell of charge) is given by:
\begin{equation} \Vec g = \begin{cases}
0&\textrm{for } r<a\\ -G \,\frac{M}{b^3-a^3}\,\left( r-\frac{a^3}{r^2}\right)\, \hat r & \textrm{for } a<r<b\\
- G\,\frac{M}{r^2}\, \hat r & \textrm{for } r>b \\
\end{cases} \end{equation} (If you want extra practice with Gauss's law, this is a good question to practice on!)
This problem explores the consequences of the divergence theorem for this shell.
Using the given value of the gravitational field, find the divergence of the gravitational field everywhere in space. You will need to divide this question up into three parts: $r<a$, $a<r<b$, and $r>b$.
Discuss the physical meaning of the divergence in this particular example.
For this gravitational field, verify the divergence theorem on a sphere, concentric with the shell, with radius $Q$, where $a<Q<b$.
Discuss how this example would change if you were discussing the electric field of a uniformly charged spherical shell.
- (DivergencePractice2)
Choose some simple vector fields of your own and find the divergence of them both by hand and using Mathematica or Maple. Choose some that are written in terms of rectangular coordinates and others in cylindrical and/or spherical.
- (DivergenceVisualizePractice)
If you need more practice visualizing divergence, go through the Mathematica notebook on the course website.
Homework for Static Fields
- (GaussLawDifferential)
For an infinitesimally thin cylindrical shell of radius $b$ with uniform surface charge density $\sigma$, the electric field is zero for $s<b$ and $\vec{E}= \frac{\sigma b}{\epsilon_0 s}\, \hat s$ for $s > b$. Use the differential form of Gauss' Law to find the charge density everywhere in space.