Ampère's Law
In-class Content
- Ampère's Law and Symmetry Argument (Lec - 20 min)
- Ampère's Law (SGA - 50 min)
Homework for Static Fields
- (Stokes) Long problem where to verify Stokes' Theorem by comparing the flux of the curl of the magnetic field for a cylindrical wire with the closed line integral of the magnetic field around a loop. Ampere's Law is required to solve several sections of this problem.
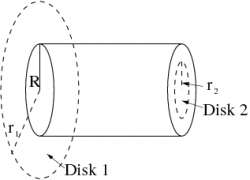
In this problem, you will be investigating, from several different points of view, a cylindrical wire of finite thickness $R$, carrying a non-uniform current density $J=\kappa s$, where $\kappa$ is a constant and $s$ is the distance from the axis of the cylinder.\\
Find the total current flowing through the wire.\\
Use Ampère's law in integral form to find the magnetic field at a distance $r_1$ outside the wire.\\
Use Ampère's law in integral form to find the magnetic field at a distance $r_2$ inside the wire.\\
Use theta functions to write the magnetic field everywhere (both inside and outside of the wire) as a single function.\\
Evaluate $$\int \left(\grad\times\BB\right)\cdot d\AA$$ for Disk 2, a circular disk of radius $r_2<R$. Use this result and part (d) to verify Stokes' theorem on this surface.\\
Evaluate $$\int \left(\grad\times\BB\right)\cdot d\AA$$ for Disk 1, a circular disk of radius $r_1>R$. Use this result and part c) to verify Stokes' theorem on this surface.\\