You are here: start » courses » lecture » pplec » pplecrevcircuitde
Review of Differential Equations in Circuits (5 minutes)
- The differential equations defining charge (or current, if you wish) in basic circuits as a function of time are found using Kirchoff's Current Law and Kirchoff's Voltage Law. Using Kirchoff's Voltage law, we can find that:
$$V_{L}=L\frac{dI}{dt} \; \; ,$$
and
$$V_{C}=\frac{Q}{C} \; \; .$$
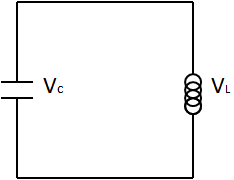
Now, as an example of Kirchoff's Voltage Law, if we combine a capacitor and an inductor in series as shown below,
we find that
$$V_{C}+V_{L}=0 \; \; ,$$
which implies that
$$\frac{Q}{C}+L\frac{d^{2}Q}{dt^{2}}= 0 \; \; .$$
This differential equation will define what the charge in the circuit will do.
So, the main strategy for solving for $Q(t)$ in a simple circuit made from inductors, capacitors, and resistors is to look for the differential equation and solve it.
NOTE: Resistors, capacitors, and inductors in series and parallel all have different properties from one another. Remind students to find review these properties again.