You are here: start » courses » lecture » eelec » eelecrevieweneigenv
Lecture: Reviewing Several Energy Eigenvalues (10 minutes)
- Review the different eigenvalues covered in the previous quantum paradigms
- Particle in a box
- Harmonic oscillator
- Rotating molecules
Lecture notes from Dr. Roundy's 2014 course website:
I'm going to quickly review and introduce the energy eigenvalues for some simple quantum mechanical problems. For each of the following, I will sketch out the potential, then sketch the wavefunctions and the spacing of the energy levels.
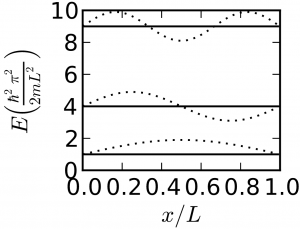
The first problem you handled was a particle in an infinite square well potential: $$\mathcal{H} = \frac{-\hbar^2}{2m}\frac{\partial^2}{\partial x^2}$$ $$E_n = \frac{\hbar^2 \pi^2 n^2}{2m L^2}$$ where $n≥1$. We could solve the same problem in three dimensions, and the three coordinates would separate (i.e. we could use separation of variables), and we would have: $$\mathcal{H} = \frac{-\hbar^2}{2m}\nabla^2$$ $$= -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} - \frac{\hbar^2}{2m}\frac{\partial^2}{\partial y^2} - \frac{\hbar^2}{2m}\frac{\partial^2}{\partial z^2}$$ $$ E_{n_xn_yn_z} = \frac{\hbar^2 \pi^2 \left(n_x^2 + n_y^2 + n_z^2\right)}{L^2}$$
Rigid rotor
The next moderately simple problem is the rigid rotator. In this case, the only energy in the Hamiltonian is the angular kinetic energy: $$\mathcal{H} = \frac{-\hbar^2}{2I}L^2$$ $$E_{lm} = \frac{\hbar^2 l(l+1)}{2I}$$
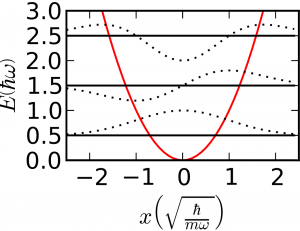
Finally, we have a simple problem that hasn't yet come up in the paradigms, which is the simple harmonic oscillator. In this case we have both kinetic and potential energy: $$\mathcal{H} = \frac{-\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + \frac{m\omega_0^2}{2}x^2$$ $$E_{n} = \left(n + \frac12\right)\hbar \omega_0$$ Of course, you also studied the hydrogen atom, but its solution is less general than those we've listed here. Any diatomic molecule behaves like a rigid rotator and a simple harmonic oscillator, and like a particle in a box, too!