You are here: start » courses » lecture » eelec » eeleccarnoteff
Lecture: Carnot Efficiency (30 minutes)
- There should be an inclusion of how having a machine more efficient than the Carnot Efficiency would violate the second law
- Coverage of both heat engines and refrigerators is recommended
- This could be skipped or covered quickly, but keep in mind homework refers to Carnot efficiency.
Lecture notes from Dr. Roundy's 2014 course website:
A heat engine is a device that accepts energy in the form of heat from something hot, and uses that energy to do work. The Kelvin formulation states that this cannot be all that a heat engine does. In fact, a heat engine will also “waste” energy by heating something cool. Thus the energy you put in from the “hot place” will not all get used to do useful work.
I will diagram heat engines as displayed in this picture. The heat engine contains several parts. 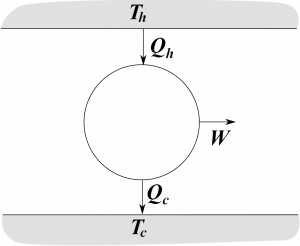
- At the top and bottom are hot and cold heat sinks. The operator of the engine has to keep these two heat sinks at fixed temperature, which means burning fuel to warm up the hot sink, and using something like a radiator to keep the cold sink cool.
- In the middle of the picture is the engine itself, which will contain some sort of a working substance that is (most likely) alternately heated and cooled.
- There is some amount of heat $Q_h$ transferred from the hot sink to the engine, and some other amount of heat $Q_c$ (both taken to be positive numbers) transferred from the engine to the cold sink. By the first law, the difference between these must be the work.
$$W=Q_h-Q_c$$ It may seem like heat engines (and steam engines) are a bit old-fashioned, but about 80% (according to wikipedia) of electric power in the world is generated by steam turbines, which are simple heat engines. So it's not really a 19thth century application, although it was pretty well understood in the 19thth century.
Efficiency
The efficiency in general is what you get out divided by what you put in. In this case, what we have to put in is the heat added to the hot reservoir $Qh$, and what we get out is the work $W$, so $$\eta = \frac{W}{Q_h}$$ $$= \frac{Q_h - Q_c}{Q_h}$$ $$= 1 - \frac{Q_c}{Q_h}$$ So clearly, we'd like to minimize the amount of heat sent to the cold sink. This also has environmental advantages.
If each step is done reversibly, then we could run a heat engine in reverse, and have a refridgerator. Thus we put do work on the fridge, and cool off the cold sink, while warming up the hot sink. 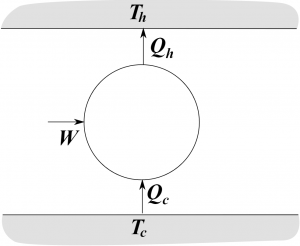
The efficiency of any reversible heat engine must be the same as the efficiency of any reversible refridgerator. We can see this by using a heat engine to drive a refridgerator. By choice the work done by the engine is the same as the work done on the fridge. If the efficiencies of the fridge and engine differ, then there will be a net transfer of heat either from hot sink to cold sink or from cold sink to hot sink. The former would be reasonable and natural, but the latter would be crazy, which means that the fridge cannot be more efficient than the engine. However, if both fridge and engine are reversible, then if the fridge is less efficient than the engine, then we could run the thing in reverse, and get the crazy situation again happening, in which nothing changes except that heat is transferred from a cold place to a hot place… and that just isn't natural!
So we can only conclude that every possible reversible heat engine must have the same efficiency!
For a reversible engine, the net entropy change of system plus surroundings must be zero over each cycle. Since the entropy change of the system is always zero, even for an irreversible engine, we only need consider the entropy change of the surroundings.