You are here: start » activities » guides » wvreftrananim
Navigate back to the activity.
Reflection and transmission animation: Instructor's Guide
Main Ideas
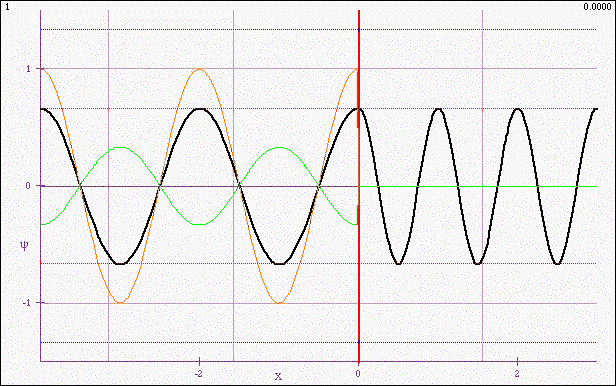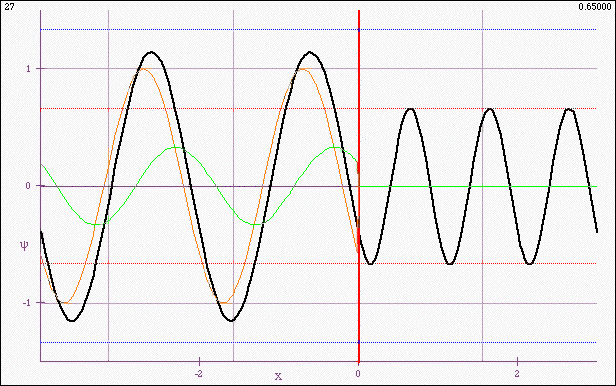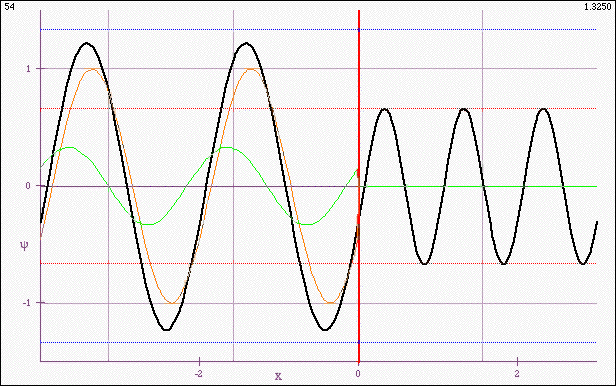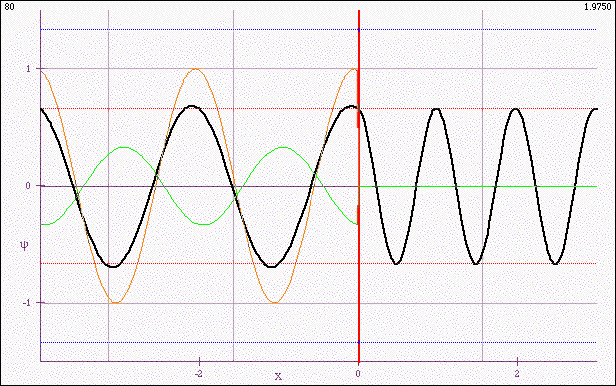
Vizualization of a sinusoidal wave incident from the left on an abrupt boundary. The wave is reflected and transmitted, with the wave on the left being a superposition of the incident and reflected sinusoids and hence neither pure traveling nor pure standing (except for two special cases).
Students' Task
Estimated Time: 15 minutes
The students' task is to ask questions. With a little management, a class discussion will ensue, with the instructor prompting new discussion when and if necessary. Emphasize (and record, if time is available) the important points as they emerge.
Prerequisite Knowledge
Knowledge of wave language, direction of travel. The activity may be done either before or after a mathematical discussion of the phenomenon.
Props/Equipment
- The animation below, displayed to the class
- (optional) Computers with Maple or Mathematica for students to work in groups, if desired
Activity: Introduction
The instructor shows the animation, explaining that the thick black waveform is the profile of the rope that is actually seen, and that the thinner, colored profiles (on the left) are components representing the incoming (orange) and reflected (green) waves. (The important point is that the animation should work well - it should be smooth, of good resolution and easy to see. In the present version, there is a particular set of conditions shown. There is a supplementary version that allows parameters to be varied. I prefer to have a single version for this first conversation.)
Activity: Student Conversations
- The wave on the left “breathes” or “hops” (the students' words). Students know that traveling waves can be superposed, but they haven't really though about what the superposition looks like in real time, except possibly in the case of a hard or soft boundary, where the resultant wave on the left is a pure standing wave. One van introduce the term “standing wave ratio” (an engineering term) to characterize the extent to which the superposition is a pure standing wave.
- The continuity of the slope at the boundary. Students are surprised to see that such continuity is possible. The continuity of the rope itself is no surprise, but the slope continuity is not something they've seen in real time before. They are also surprised to see how wave form of one wave length can smoothly connect connect to a waveform of another wavelength.
- Students are surprised that the point on the boundary does not exhibit the full range of motion of the incident wave, i.e. it matches the amplitude on the right, but not on the left.
- The breakdown of the resultant left-hand-side wave form into incident and reflected traveling waves is important. Students can see that these are pure traveling waves, of different amplitude (the dashed colored lines that indicate the maximum (blue) and minimum (red)extensions are useful) and that they superpose to create something that is not a pure traveling wave.
Activity: Wrap-up
The students should make their own list of the important points that they have gleaned from the exercise (unless you've recorded them on the board), and any further questions they have. Ask students to read out points from their lists, and continue until they have covered all the points you have on yours. If you have already recorded the important summary points, reiterate them, and ask the students how the animation gave them new insights. A very important message to convey is that they should become used to making animations themselves to see how waves behave.
Extensions
- Ask the students to work independently with their own copy of the animation, one that allows the wave velocities on each side of the boundary to be altered. They can investigate the effect of changing the parameters to the limits where (i) both ropes are identical (ii) the right hand rope is much denser (iii) the right hand rope is much less dense - or absent.