You are here: start » activities » guides » osintialconditions
Navigate back to the activity.
Initial conditions: Instructor's Guide
Main Ideas
- To familiarize students with the expression $y(t) = B_p cos \omega t + B_q sin \omega t$
- To recognize that $y(t) = A cos (\omega t + \varphi)$ and $y(t) = B_p cos \omega t + B_q sin \omega t$ represented the same expression.
- To find the relationships between arbitrary constants.
Students' Task
Estimated Time: 15 minutes
The students were presented with initial conditions for an oscillating system in the picture and asked to express the motion of the mass in the form A and B. 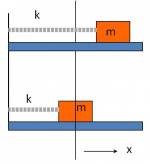
Prerequisite Knowledge
- Solving ODE.
- Trig identities.
Props/Equipment
- Tabletop Whiteboard with markers
- A handout for each student osintialconditionshand.pdf.
Activity: Introduction
The two representations will have been introduced in a short lecture. Students count off into groups of 3-4, and groups are assigned one representation. Groups are asked for the values of the constants given the initial conditions. Groups proceed to the other representation if they finish early.
Activity: Student Conversations
Students have to remember to differentiate to get the velocity from the position. Someone in the group invariably knows this, and some others invariably forget.
Applying the initial conditions to come up with two simultaneous equations is obvious to the expert; some groups need time to think this through. If the initial conditions assigned are those at t = 0, the groups assigned to the “B-form” are pleasantly surprised at how easily the constants are revealed.
Students wrestle with units if the amplitude (e.g. mm) is given in units that do not immediately correspond to those of the velocity (e.g. m/s).
Activity: Wrap-up
Groups report on their findings. Expect numerical inconsistencies, which the groups can resolve. The main point is that both representations give the same motion (this can be easily demonstrated using Maple), and that there is a well-defined relationship between the \(\left( A,\varphi \right)\) and the \(\left( B_{p},B_{q} \right)\) constants. A quick derivation of this using the standard trig expansions can be done on the board or the students can do it in their groups.
Extensions
More complicated initial conditions (e.g. those at $t\neq 0$ can be given. This doesn't usually add much, but may be useful if students feel that the above exercise is too much in the way of review.