Guessing the Fourier Expansion of a Function
Highlights of the activity
- This computer visualization activity is designed to help upper-division undergraduate students understand superposition and Fourier series.
- Students used Maple/Mathematica to guess the terms of a Fourier series and compared to a plot of an assigned function that was the superposition of two or more harmonic functions.
- The wrap-up discussion focuses on the idea of superposition and introduces students to the idea of Fourier Expansion.
Reasons to spend class time on the activity
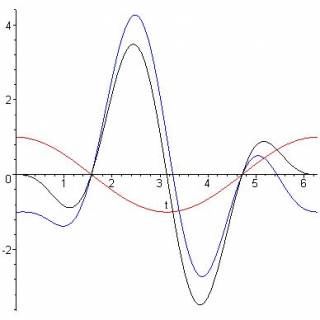
This is a short Maple/Mathematica worksheet that plots an oscillatory function and asks the students to guess the representative Fourier series, which they plot and compare to the original. They are told that the series has three sine terms with integer coefficients. The idea is that students develop a feeling for what a Fourier series looks like graphically, rather than just as a mathematical expression, and for what graphical aspects are important (e.g., amplitude, zero-crossings, curvature changes). The activity is short enough to give the students control of the Maple/Mathematica code. An important aspect of this activity is that students must have a good grasp of what it means to add functions together, which they may not have done explicitly before.
Reflections
Instructor's Guide
Maple Worksheet
osfourierguess.mw (Maple 13)
osfourierguess.mws (Maple 11 Classic)