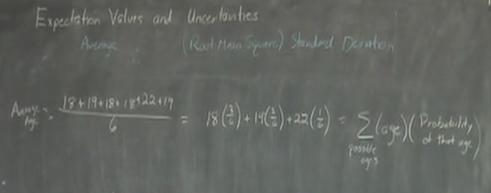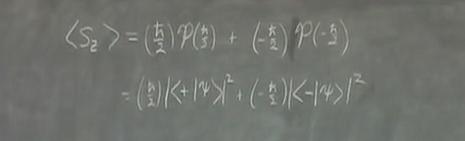Expectation Values & Quantum Uncertainty (15 minutes)
spins_unit_operators_and_measurements.ppt Pages 29-33, 38
- Introduce that the topic will be on expressing averages and uncertainty in quantum mechanical systems (i.e. expectation values and quantum mechanical uncertainties).
- Start by presenting how most students think of averages. In the case of the average age of six students, the age of each student is added together and this value is divided by six. Then, show how this data can be manipulated to look like the expectation value way of considering averages.
- Now, perform a quantum mechanics example by finding the expectation value of $S_{z}$. Start by writing the probabilities only in terms of $P_{\frac{+ \hbar}{2}}$ and $P_{\frac{- \hbar}{2}}$. Then, write the probabilities in terms of bra-ket notation.
- From the proof of the Completeness Relation, move backwards from the bra-ket probabilities and write each probability as the state projected onto $\vert+ \rangle$ or $\vert- \rangle$ times its complex conjugate. This looks like
$$\frac{+ \hbar}{2}\langle \psi \vert +\rangle\langle+ \vert\psi \rangle \; \; + \; \; \frac{- \hbar}{2}\langle\psi \vert- \rangle\langle -\vert\psi \rangle \; \; . $$
We can reverse FOIL the expression above (again, referencing the completeness relation proof helps for students to see the operation) and pull out the $\vert\psi \rangle$ terms to acquire
$$\langle\psi \vert \left(\frac{+ \hbar}{2}\vert +\rangle\langle+ \vert \; \; + \; \; \frac{- \hbar}{2}\vert- \rangle\langle -\vert\right)\vert\psi \rangle \; \; . $$
Now, the terms in the parentheses can be re-written with the according spin operators using the eigenvalue equation. This changes the expression to
$$\langle\psi \vert\left(\hat{S_{z}}\vert +\rangle\langle+ \vert \; \; + \; \; \hat{S_{z}}\vert- \rangle\langle -\vert\right)\vert\psi \rangle \; \; . $$
The $\hat{S_{z}}$ can be factored out of the expression in the parentheses, and all that will be left in the parentheses is the completeness relation. Thus, our expectation value can be written as
$$\left\langle\hat{S_{z}}\right\rangle \; = \; \langle\psi \vert\hat{S_{z}}\vert\psi \rangle \; \; . $$
- Having some way to tell on average how close each point is to the average value of the data is very important. Since the distance between points is found with a difference, we can expect the uncertainty to have a subtraction of each data point from the average value of the data. To omit any minus signs, we'll need to square the value and take the square root again. Points that are more probable contribute more to the uncertainty value as well, so a probability term should come up. Write on board
$$Uncertainty \: = \: \sqrt{\sum_{i}\left(a_{i}-\left\langle \hat{A}\right\rangle \right)^{2}P(a_{i})} \; \; . $$
Notice the term inside the square root looks just like an expectation value: an expression times a probability. Thus, we can re-write the uncertainty to take the form
$$Uncertainty \: = \: \sqrt{\left\langle \left(a_{i}-\left\langle \hat{A}\right\rangle \right)^{2}\right\rangle} \; \; . $$
Now, the squared expression inside the expectation value can be expanded and the sums resulting from the expectation value can be carried through to yield
$$Uncertainty \: = \: \sqrt{\left\langle a_{i}\right\rangle ^{2}-2\left\langle a_{i}\right\rangle\left\langle\hat{A}\right\rangle-\left\langle\hat{A}\right\rangle^{2}} \; \; . $$
Finally, the expectation value of the data points is the average of the operator, which makes $\left\langle a_{i}\right\rangle =\left\langle \hat{A}\right\rangle $. When we make this substitution, the uncertainty simplifies to take the most common form
$$Uncertainty \: = \: \sqrt{\left\langle\hat{A}^{2}\right\rangle-\left\langle\hat{A}\right\rangle ^{2}} \; \; . $$