Differences Between Vibrating Atoms and Electrons in a Crystal (5 minutes)
- Vibrations of atoms in a crystal:
- Boundary conditions result in normal modes (envelope functions where all atoms move with the same frequency).
- Time dependence: $e^{i \omega t}$.
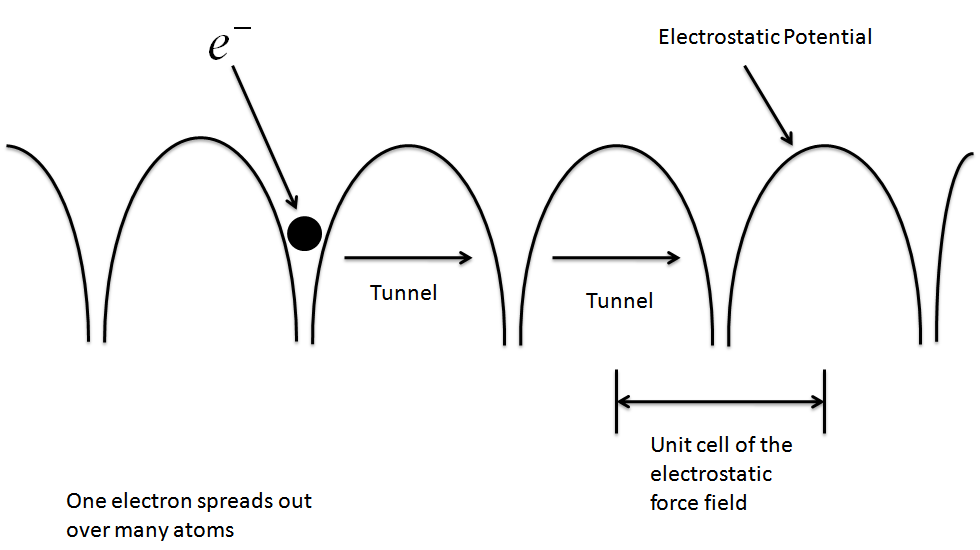
- Electrons in a crystal:
- Boundary conditions result in eigenstates (eigenstates are the analog of normal modes).
- Time dependence evolves from the Schrodinger Equation: $e^{i\frac{E}{\hbar}t}$.