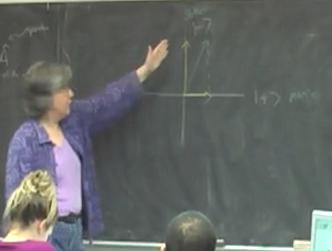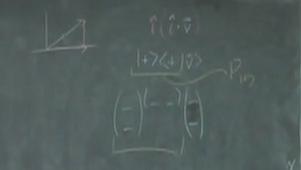The Projection Operator & Wave State Collapse (30 minutes)
- Ask the class what they know about projections in any context.
- Tell the students that when you sort the particles using the Stern-Gerlach device, the particles leave the device in the quantum state corresponding to that sorter. This is called the collapse of a wave state.
- To provide a visual representation of what happens in a wave state collapse, draw a 2-space diagram with dimensions $\vert+ \rangle$ and $\vert- \rangle$. Draw some arbitrary state that is a linear combination of the two and project the vector onto one of the axes.
- Emphasize that this projection of a wave state onto one of the axes is the graphical representation of what occurs in the collapse of a wave state.
- Be sure to emphasize that after performing the projection onto a state, the new wave state needs to be normalized.
- The projection onto different wave states operates in the same manner as well, only the wave states are projection onto different axes. Draw the $\vert+ \rangle_{x}$ ket graphically and show how a wave state can be projected onto it.
- Now, tell the students we need an operator that will mathematically perform this projection on a wave state. Unfortunately, we cannot do this with an operator similar to $S_{x}$ or $S_{z}$, so one of the goals will be to find this projection operator.
- At this point, give to students that if $\vert\psi \rangle$ represents some incoming wave state, $\vert\psi '\rangle$ represents the outgoing wave state, and $P_{\vert\psi ' \rangle}$ represents the projection operator that projects wave states onto the new state $\vert\psi ' \rangle$, the outgoing wave state is found using the expression
$$\vert\psi ' \rangle=\frac {P_{\vert\psi ' \rangle} \vert\psi \rangle}{\sqrt{\langle \psi|P_{\vert\psi ' \rangle}\vert\psi \rangle}} \; \; . $$
Unfortunately, there's no mathematically nice way to do this operation; to find the projection, the only choice is to plug in what we know and grind through computing the bra-kets.
- Emphasize, however, that we oftentimes already know the answer. For example, if the outgoing state is $\vert+ \rangle_{x}$, we already know that any wave stated projected onto it and normalized will be represented in the z-basis as
$$\vert+ \rangle_{x}=\frac{1}{\sqrt{2}}\vert+ \rangle + \frac{1}{\sqrt{2}}\vert- \rangle \; \; . $$
- Now, ask if any students can guess what $P_{\vert+ \rangle}$ and $P_{\vert- \rangle}$ may be (this can be asked as a small white board question if you wish). Generally, a student will find that
$$P_{\vert+ \rangle}\dot = \left(\begin{array}{cc} 1 & 0 \\ 0 & 0 \\ \end{array}\right)\; \; \; \; \text{and} \; \; \; \; P_{\vert- \rangle}\dot =\left(\begin{array}{cc} 0 & 0 \\ 0 & 1 \\ \end{array}\right) \; \; .$$
- Now, the projection operators $P$ for the x-oriented and y-oriented devices would look exactly the same in their own basis, but we want to find the projection operators for both orientations in the z-basis. To do this, it is actually easier to try to find the operator in terms of bra-ket language.
- Show the students how the projection operator has an analog in cases dealing with vectors. Work through performing a projection in a vector space, and then change the operation into bra-ket terms that deal with states.
- Note that the order of the bra-kets for the projection operation appears bizarre, but this placement groups together the projection components. Also, with this order, a 2×2 projection matrix (which would have the form of operators like $S_{x}$) can be found using the outer product.