Infinite Chain of One-Dimensional Diatomic Molecules (40 minutes)
- When we analyzed the infinite monatomic chain of particles, the dispersion relation was found using the equation of motion given by the forces on the particle, which was found to be
$$m\ddot{x}_{n} \, = \, -\kappa\left(x_{n}-x_{n-1}\right) - \kappa \left(x_{n}-x_{n+1}\right) \; \; .$$
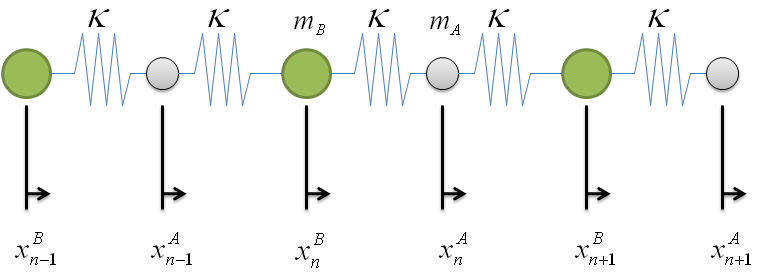
- Now, let's consider an infinite diatomic chain, found below.
- Now, the monatomic chain was described by one equation of motion. However, the diatomic chain has two different particles in each unit cell; thus, we can expect this system to need two differential equations to describe the motion completely and yield a dispersion relation. Looking at the displacements of each particle in the diagram above, we can find that the equations of motion for the two molecules in the $n$th unit cell are
$$m_{A}\ddot{x}_{n}^{A} \, = \, -\kappa\left(x_{n}^{A}-x_{n-1}^{B}\right) - \kappa \left(x_{n}^{A}-x_{n}^{B}\right) \; \; $$
and
$$m_{B}\ddot{x}_{n}^{B} \, = \, -\kappa\left(x_{n}^{B}-x_{n}^{A}\right) - \kappa \left(x_{n}^{B}-x_{n+1}^{A}\right) \; \; .$$
Note the different masses for each force equation; this is an important distinction for the diatomic case. Simplifying these expressions, we receive two coupled D.E.s:
$$m_{A}\ddot{x}_{n}^{A} \, = \, \kappa\left(x_{n-1}^{B}-2x_{n}^{A} + x_{n}^{B}\right) \; \; ,$$
$$m_{B}\ddot{x}_{n}^{B} \, = \, \kappa\left(x_{n}^{A}-2x_{n}^{B} + x_{n+1}^{A}\right) \; \; .$$
- We now need to describe the position functions for each molecule in a unit cell. Just like the monatomic case, we can use sinusoidal envelope functions, where
$$x_{n}^{A}=C_{A} \, \sin{kna}$$
and
$$x_{n}^{B}=C_{B} \, \sin{\left(kna+\delta_{k}\right)} \; \; .$$
Note that the second particle in the unit cell has a phase factor $\delta_{k}$ in the sine function. This phase factor is necessary to set the phase difference in the motion of the A and B atoms for each particular envelope function. Without it, both particles would start at the exact same displacement from their origin for every wave vector (which isn't true).
However, expressing the wave functions in complex polar form will make future calculations easier, so let's use the forms
$$x_{n}^{A}=Re\left[D e^{ikna}\right] \; \; $$
and
$$x_{n}^{B}=Re\left[\alpha D e^{ikna}\right] \; \; , $$
where $t=0$ for both statements and $D$ is a complex constant. The $\alpha$ term is called the “form factor” and has the form
$$\alpha=\alpha_{0}e^{i\delta_{k}} \; \; . $$
If any student asks, “Why use a form factor rather than two constants like we are used to?”, inform them that the form factor makes manipulating the coupled D.E.s easier because the D constant can be factored out. If they're still confused, tell them to allow you to continue the derivation and show them.
- Now, we can add the time dependence of a normal mode to our position expressions:
$$x_{n}^{A}=D e^{ikna}e^{i\omega_{k}t} $$
$$x_{n}^{B}=\alpha D e^{ikna}e^{i\omega_{k}t} \; \; .$$
- Remind the students that the ultimate goal of this derivation is to find a dispersion relation $\omega_{k}(k)$. Let's combine our position equations with the equations of motion to see if we can find $\omega_{k}$. Doing this gives the coupled D.E.s
$$-m_{A}\omega_{k}^{2}e^{ikna} \, = \, \kappa \left(\alpha e^{ik(n-1)a} \, - \, 2e^{ikna} \, + \, \alpha e^{ikna}\right) \; \; $$
and
$$-m_{B}\omega_{k}^{2}\alpha e^{ikna} \, = \, \kappa \left(e^{ikna} \, - \, 2\alpha e^{ikna} \, + \, e^{ik(n+1)a}\right) \; \; .$$
Notice that using $D$ and $\alpha D$ for the coefficients allowed for us to factor out $D$ from each equation. Ask the class how many unknowns are in these equations and what they are. Note that using a form factor was crucial; thanks to our form factor, we now have two coupled equations and only two unknowns ($\omega_{k}$ and $\alpha$).
- We can now rearrange each differential equation to solve for $\alpha$. Solving for $\alpha$ yields the expressions
$$\alpha \, = \, \frac{2\kappa - m_{A}\omega_{k}^{2}}{2\kappa\; \cos{\left(\frac{ka}{2}\right)}e^{-i\frac{ka}{2}}} \; \; $$
and
$$\alpha \, = \, \frac{2\kappa\; e^{i\frac{ka}{2}}\cos{\left(\frac{ka}{2}\right)}}{2\kappa - m\omega_{k}^{2}} \; \; . $$
Now, we can set the expressions equal to each other to eliminate the form factor $\alpha$. Rearranging the expression to solve for $\omega_{k}$ will give the dispersion relation
$$\omega_{k}(k)=\sqrt{\kappa\left(\frac{m_{A}+m_{B}}{m_{A}m_{B}}\right) \pm \kappa \left[\left(\frac{m_{A} + m_{B}}{m_{A}m_{B}}\right)^{2}-\frac{4}{m_{A}m_{B}}\sin{^{2}\frac{ka}{2}}\right]^{\frac{1}{2}}} \; \; ,$$
where $a$ is the size of a unit cell, $\kappa$ is the effective spring constant between each atom, and $k$ is the wave vector of the envelope function. Also note the appearance of the inverse of the reduced mass, where the reduced mass is defined as
$$m_{red}=\frac{m_{A}m_{B}}{m_{A}+m_{B}} \; \; .$$
- This is a good time to perform the Optical and Acoustic Branches of an Infinite Diatomic Chain activity with the class.
- Draw a general figure of the dispersion relation on the board as seen below.
Ask the class about any important features of the dispersion relation they can see. Important observations of dispersion relation:
- Neither branch of the dispersion relation is linear.
- The presence of the $\pm$ sign introduces two distinct branches to the dispersion relations: the optical and acoustic branches.
- Between the two branches, there is now a band of vibrational frequencies that are forbidden in the oscillator.