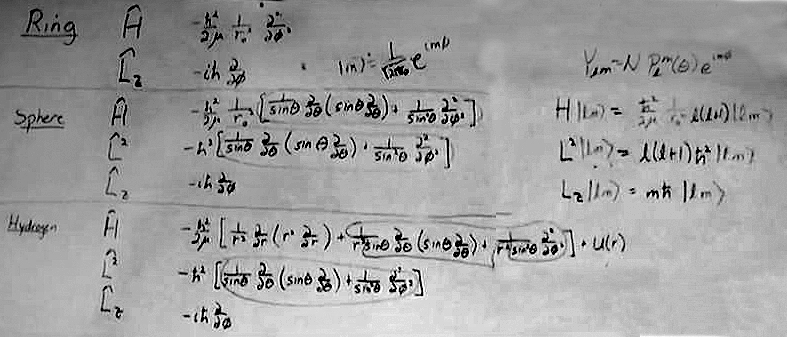Central Forces Notes Section 27

• The quantum mechanical angular momentum operators $L_z$ and $L^2$ are found for the ring and the sphere.
• As a sort of road map, the $H$, $L_z$ and $L^2$ operators are written in a table for the ring, sphere and hydrogen atom problems.

• The eigenvalues for the $H$, $L_z$ and $L^2$ operators are also given for the rigid rotor problem.
• It is noted that for the ring, $H$ and $L_z^2$ operators are to within a constant the same operator and that for the sphere, $H$ and $L^2$ operators are to within a constant the same operator. As we move forward we will find that the $H$, $L^2$ and $L_z$ operators are all independent for the hydrogen atom.
• The communtators between these operators are reviewed and the meaning of this commutation or non-commutation is discussed.
• Small Whiteboard Question: Write down for me on your small white boards, the eigenvalue/eigenvector equation on the sphere for the operator $L_z$. Do the same for $L^2$. Do the same for $H$. If you do this after you have talked about the energy of the hydrogen atom, it is even more helpful to ask them to do this for $\vert nlm\rangle$ states. This actually works really well as a lead in to talk about how the Hamiltonian differs for the ring, sphere, and atom.
• The matrix representations of the $H$, $L^2$ and $L_z$ operators for the sphere (rigid rotor) and ring problems are derived in the basis of the energy eigenstates. Discuss with the students possible conventions for ordering the rows and columns.
• Some time is spent building connections between the states of the ring and sphere problems with the discrete problems done in the Spins Paradigm. In particular, there is lecture/discussion about how to do quantum mechanical calculations relating to the energy and angular momentum of a particle confined to a sphere and how these calculations are similar to those done in the case of spin. The class also discusses the experiments one might do to measure energy and angular momentum for the rigid rotor.