You are here: start » courses » lecture » pplec » pplecwavestates
Energy Eigenstates of a Single Potential Well (5 minutes)
- Consider a single isolated atom (i.e. single potential well) as shown below:
- Notice that the potential well is not a square well, so our energy eigenstates will look less familiar.
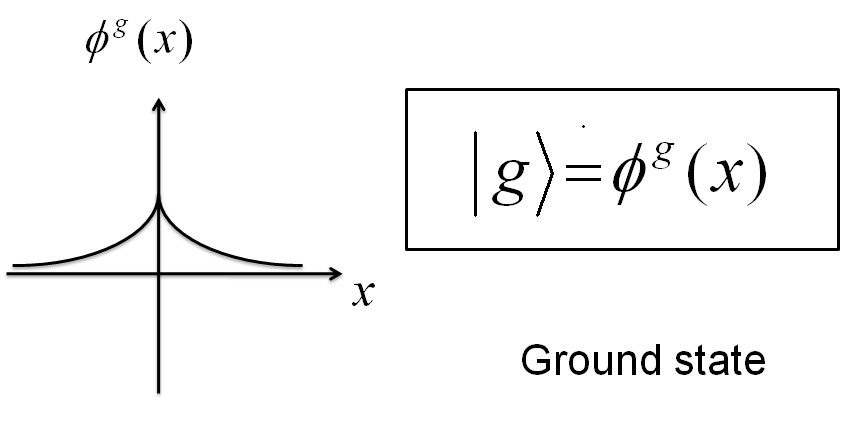
- The ground state (lowest energy eigenstate) wave function for a single well will look like:
Rather than write the exact equation for this function repeatedly throughout the course, let's represent this state as
$$\vert g \rangle \; \dot{=} \; \phi ^{g}(x) \; \; . $$
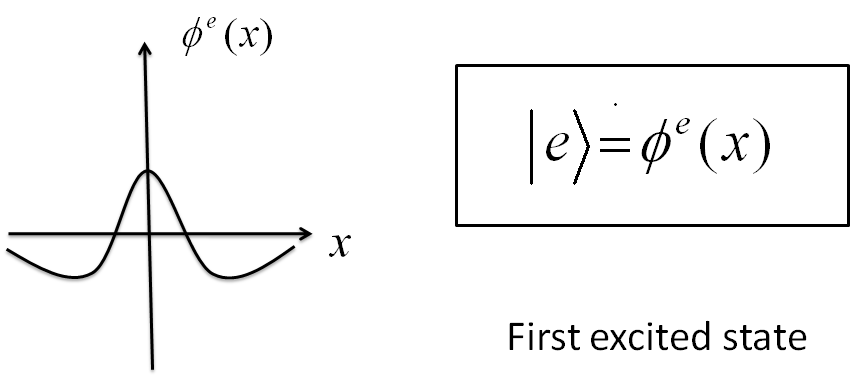
- The first excited state (second lowest energy eigenstate) wave function for a single well will look like:
Just as we did with the ground state, let's represent this state as
$$\vert e \rangle \; \dot{=} \; \phi ^{e}(x) \; \; $$
to avoid repeatedly writing down messy equations.
- Note that both of these equations are centered at zero. To center the wave function at some location $a$ (important for wells that are neighboring each other), simply replace $x$ with $x-a$ in the functions above.
- The single atom system eigenstates will be very important to our analysis of systems with many atoms. We will use the energy eigenstates for this system as a basis to work with the multi-well cases.