You are here: start » courses » lecture » pplec » pplecsingleelec
Single Electron in a Crystal (15 minutes)
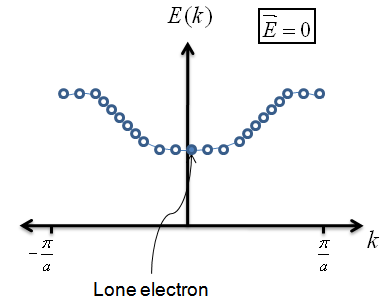
- Recall that, for a 1-D crystal of atoms, the energy of the electron is a function of the wave vector as:
$$E = \alpha + 2\beta \, \cos{ka} \; \; , $$
where we recall that $\alpha$ is a positive value and $\beta$ is a negative value.
Let's plot this energy graph.
Recall that each allowed energy value is directly related to a particular wave vector $k$. The circles in the graph represent these discrete allowed energies.
For the above graph, there is no electric field applied across the crystal. Because of this, the electron sits in the lowest energy eigenstate possible and isn't moving anywhere (i.e. it is delocalized over a finite region of space).
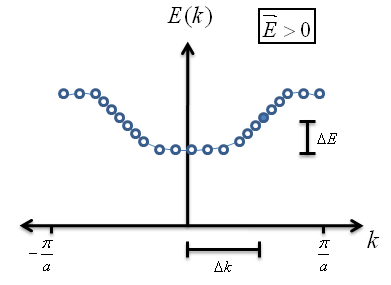
- What will happen if we apply an electric field across the crystal? When we apply a charge across a metal wire, it induces a flow of electrons; we should expect the same to happen here if it's a conductor.
We can see that the electric field increases the energy (and, in turn, the wave vector) of the electron. As expected, the electron is also accelerated across the crystal when the electric field is turned on. This crystal is a conductor.
- Note that after a few pico seconds of exposure to the electric field, the electron reaches “terminal velocity.” This occurs because momentum is lost in scattering events as quickly as the electric field provides acceleration.