Periodic Boundary Conditions on Long Chains of Atoms (15 minutes)
- For the potential landscapes we have recently been analyzing, the boundary conditions on each end of the atomic chain have been pivotal to what wave vector values $k$ are allowed. However, for atomic chains that are on the scale of $10^{23}$ atoms, material properties deep in the middle of the chain should not necessarily depend on what's occuring at the very edges. This motivates the use of periodic boundary conditions.
- To satisfy periodic boundary conditions, we will focus only on a single unit length of an atomic chain that has $N$ potential wells confined within it.
The two important conditions that must be satisfied for periodicity:
- The coefficients for $\vert 1 \rangle$ and $\vert N \rangle$ must be the same.
- The same condition must also apply to any analysis on any other unit length on the chain (i.e. $\vert 2 \rangle$ and $\vert N+1 \rangle$, $\vert 3 \rangle$ and $\vert N+2 \rangle$, etc.).
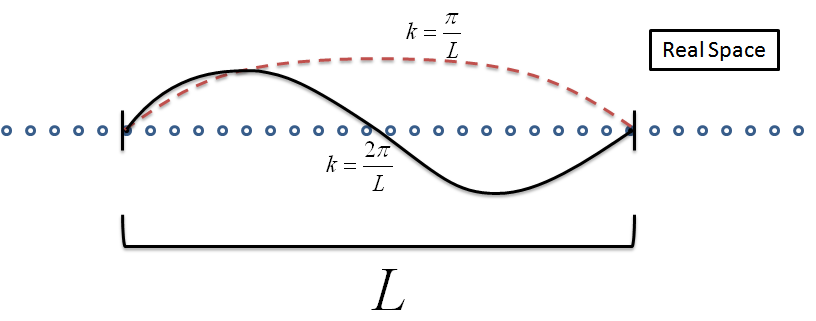
The first condition essentially tells us that if we continued the envelope function past our unit length, it must be continuous and smooth. Let's see if $k=\frac{\pi}{L}$ or $k=\frac{2\pi}{L}$ satisfy this condition.
Notice that $k=\frac{\pi}{L}$ is not an allowed envelope function for periodic boundary conditions because the function is not smooth when continued past the unit length. $k=\frac{2\pi}{L}$, however, is an allowed wave vector.
Continuing this analysis, we can see that the only allowable wave vectors for our LCAO are
$$k=\frac{2\pi}{L}, \frac{4\pi}{L}, \frac{6\pi}{L}, …$$
- With these conditions in mind, we can now limit our set of orthogonal LCAO eigenstates to
$$\sum_{n=1}^{N} A\, \cos{(kna)}\; \phi (x-na) \; \; $$
$$\sum_{n=1}^{N} A\, \sin{(kna)}\; \phi (x-na) \; \; , $$
$$k=\frac{2\pi}{L}, \frac{4\pi}{L}, \frac{6\pi}{L}, …$$
Equivalently, these can be written as
$$\sum_{n=1}^{N} A\, e^{ikna}\; \phi (x-na) \; \; $$
$$\sum_{n=1}^{N} A\, e^{-ikna}\; \phi (x-na) \; \; , $$
$$k=\frac{2\pi}{L}, \frac{4\pi}{L}, \frac{6\pi}{L}, …$$
We can also combine the complex polar forms into one master representation as
$$\sum_{n=1}^{N} A\, e^{ikna}\; \phi (x-na) \; \; ,$$
$$k=\frac{-N\pi}{L}, … ,\frac{-2\pi}{L},0, \frac{2\pi}{L}, \frac{4\pi}{L}, … , \frac{N\pi}{L} \; \; .$$
Note that the sign of the wave vector determines the direction of the traveling wave.
$$k < 0 \; \text{is a traveling wave with momentum leftward.}$$
$$k > 0 \; \text{is a traveling wave with momentum rightward.}$$
- Ask the class this question: looking at the master representation for LCAO eigenstates, how many eigenstates exist in an arbitrary unit length of the atomic chain? If any students asks, remind them that we are only using the ground state functions for $\phi(x-na)$, so there will be no additional energy eigenstates due to excited states.
Show them that the number of eigenstates is equal to the number of k-values that the electron's envelope function can possibly take. Classically, the number of eigenstates can be related to finding the number of modes of a chain of masses.
$$\text{# eigenstates} \; = \; \frac{\text{# k-values}}{\text{spacing}}\; = \; \frac{\frac{2N\pi}{L}}{\frac{2\pi}{L}} \; = \; N \; \; .$$