You are here: start » courses » lecture » pplec » pplecnwellsys
Finding the Energy Eigenstates of an N-Well System (40 minutes)
- Before beginning this lecture, it is recommended that students be shown how to find the Hamiltonian for the n-well system.
- Now, for the n-well system, we have the n $x$ n Hamiltonian
$$H \; \dot{=} \left[\begin{array}{ccccc} \alpha & \beta & 0 & 0 & \dots\\ \beta & \alpha & \beta & 0 & \\ 0 & \beta & \alpha & \beta & \ddots \\ 0 & 0 & \beta & \alpha & \ddots \\ \vdots & & \ddots & \ddots & \ddots \\ \end{array}\right] \; \; . $$
Our goal: Find the possible eigenstates of the electron in the potential landscape and the energy of each eigenstate.
- To do this, let's again use the energy eigenvalue equation
$$H\vert \psi \rangle = E \vert \psi \rangle \; \; , $$
Where $\vert \psi \rangle$ is a superposition of all of the possible ground states, written as
$$\vert \psi \rangle \; = \; \sum_{i}^{n} \, c_{i}\, \vert \, i \, \rangle \; \dot{=} \; \left[\begin{array}{c} c_{1} \\ c_{2} \\ \vdots \\ c_{n} \\ \end{array}\right] \; \; . $$
Let's try to see if an unknown state with $c_{i}=1$ for all entries is an eigenvector.
$$H \vert \psi \rangle = \left[\begin{array}{ccccc} \alpha & \beta & 0 & 0 & \dots\\ \beta & \alpha & \beta & 0 & \\ 0 & \beta & \alpha & \beta & \ddots \\ 0 & 0 & \beta & \alpha & \ddots \\ \vdots & & \ddots & \ddots & \ddots \\ \end{array}\right] \left[\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \\ \vdots \\ \end{array}\right] = E\left[\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \\ \vdots \\ \end{array}\right] \; \; .$$
Performing the matrix algebra, we find that at the ends of the vector, $E=\alpha + \beta$. For every other entry in the resulting expression,however, $E=\alpha + 2\beta$. If this is a very long chain of potential wells, a state with $c_{i}=1$ is close to being an eigenstate. Would a vector with alternating values of +1 and -1 satisfy the eigenvalue equation?
- Guessing any further for eigenvectors is going to become very difficult, so let's see what we can find about the eigenenergies instead. Let's again look at the most general expression for the energy eigenvalue equation.
$$ \left[\begin{array}{ccccccc} \alpha c_{1}& \beta c_{2} & 0 & 0 & 0 & 0 & \dots\\ \beta c_{1}& \alpha c_{2}& \beta c_{3}& 0 & 0 & 0 & \\ 0 & \beta c_{2} & \alpha c_{3} & \beta c_{4} & 0 & 0 & \ddots \\ & & & \vdots & & & \\ 0 & 0 & 0 & \beta c_{p-1} & \alpha c_{p} & \beta c_{p+1} & \dots \\ & & & \vdots & & & \\ \end{array}\right] = \left[ \begin{array}{c} E c_{1} \\ E c_{2} \\ E c_{3} \\ \vdots \\ E c_{p} \\ \vdots \\ \end{array} \right] \; \; , $$
where I have multiplied the Hamiltonian and energy by the eigenvector. Now, we can see that any arbitrary $p$th coefficient (except for the ends) must satisfy
$$ E\, c_{p} \; = \; \beta\, c_{p-1} + \alpha\, c_{p} + \beta\, c_{p+1} \; \; . $$
- Recall that in the two-well case, we were able to represent the coefficients of the eigenstates in terms of an envelope function. Let's use this as motivation to guess that these coefficients will also be described by an envelope function. So,
$$c_{p} \; = \; Ae^{ikpa} \; \; ,$$
where $k$ is the wave vector of the envelope function and $p$ is the position of the basis state. Now, let's insert this expression into the energy expression.
$$E\, Ae^{ikpa} \; = \; \beta\, Ae^{ik(p-1)a} + \alpha\, Ae^{ikpa} + \beta\, Ae^{ik(p+1)a} \; \; , $$
$$ E \; = \alpha + \beta\left(e^{ika}+e^{-ika}\right) \; \; , $$
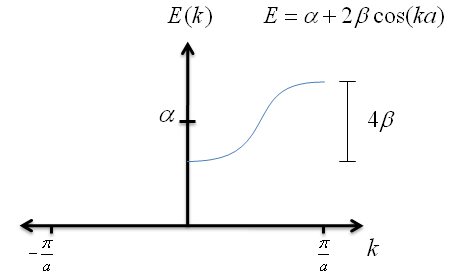
$$E \; = \; \alpha + 2\beta \cos{ka} \; \; . $$
Let's graph the the as a function of $k$.
Recall that $\beta$ has a negative value; this is very important for graphing the energy correctly. Also notice that, no matter how long the chain of potential wells is, the spread in energies never exceeds $4\beta$.
- Finally, since we know that each coefficient for an eigenstate is determined by an envelope function, we can write that the energy eigenstates corresponding to a particular wave vector $k$ are
$$\psi_{k}(x) = \sum_{p=1}^{n}A \sin{(ikpa)} \; \phi(x-pa) \; \; . $$
This function is so important, it has it's own name; it is called a Linear Combination of Atomic Orbitals (LCAO).