You are here: start » courses » lecture » pplec » pplechalfband
Half-Filled Electron Band in a Crystal (15 minutes)
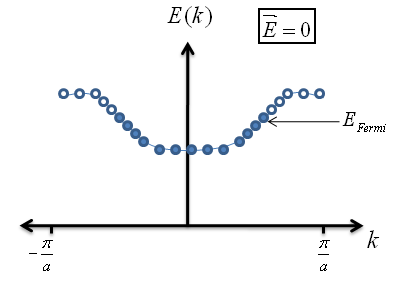
- Now, let's consider a crystal containing multiple electrons. Let's again graph our energy function $E(k)=\alpha + 2 \beta \, \cos{ka}$.
Some things to notice:
- The electrons fill the lowest energy levels first.
- The Pauli Exclusion Principle is apparent here; each electron goes into a different energy eigenstate (some have the same energy, but all have different wave vectors).
- The highest occupied energy is called $E_{Fermi}$.
- With negative and positive wave vectors present, some some electrons move left and some move right, respectively. However, the net charge across the crystal is zero.
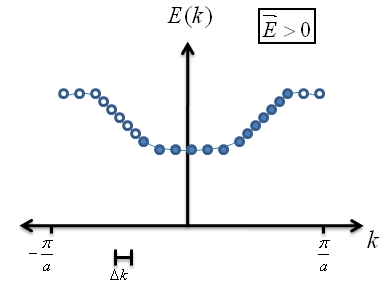
Now, let's apply an electric field across the crystal and see what happens to the electrons.
Just like the single electron band, each electron is accelerated in the presence of an electric field. Now, there are more right movers than there are left movers in the system (i.e. there are more electrons with positive wave vectors). What does this tell us about the direction of the electric field? Once again, we have a net transfer of charge across the crystal. This crystal is also a conductor.