You are here: start » courses » lecture » pplec » ppleceffmass
Effective mass (10 minutes)
Let's first consider the mass of a classical object. Some important characteristics:
- Tells us how much inertia an object has.
- Equivalently, tells us the force needed to accelerate an object.
- Equivalently, tells us how much kientic energy increases as momentum increases.
Now, for a classical object, the kinetic energy of the object is equal to
$$E \; = \; \frac{1}{2}mv^{2} \; = \; \frac{p^{2}}{2m} \; \; . $$
So if we take the derivative of the energy with respect to momentum twice, we find that
$$\frac{d^{2}E}{dp^{2}} \; = \; \frac{1}{m} \; \; . $$
- Using the de Broglie Wavelength of the electron, we can find that the electron's momentum in a crystal is related to it's wave vector by
$$p \; = \; \hbar k \; \; .$$
If we insert this into our classical notion of mass, we can find that the effective mass of the electron is
$$\frac{1}{\hbar^{2}}\frac{d^{2}E}{dk^{2}} \; = \; \frac{1}{m_{eff}} \; \; . $$
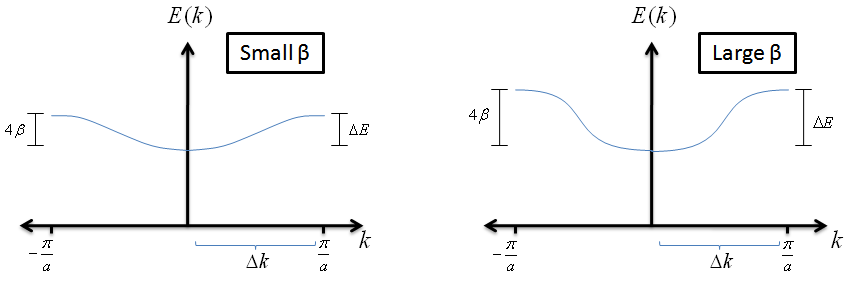
- What does this tell us about an electron in an LCAO? Let's assume we have small values of $k$ and expand the energy equation
$$E \; = \; \alpha + 2 \beta\, \cos{(ka)} \; \; , $$
$$E \; \simeq \alpha +2 \beta \left[1-\frac{1}{2}(ka)^{2}\right] \; \; , $$
$$ E \; \simeq \alpha + 2\beta - \beta a^{2}k^{2} \; \; . $$
Plugging this into our effective mass equation, we find that
$$ m_{eff} \; = \; \frac{\hbar^{2}}{-2\beta\, a^{2} \, } \; \; . $$
How can we interpret this? This expression tells us that if the $\beta$ value for an LCAO is small, the electrons behave as if they are heavier and will require more energy to achieve higher velocities. This does make mathematical sense; a small $\beta$ value means that the overlap between the atomic wave functions is small and that the electron will find it more challenging to move across the crystal.