Homework for Static Fields
- (DivergencePractice) Calculate the divergence for several made-up functions using rectangular and curvilinear coordinates.
Calculate the divergence of each of the following vector fields. You may look up the formulas for divergence in curvilinear coordinates.
$\FF=z^2\,\hat{x} + x^2 \,\hat{y} -y^2 \,\hat{z}$
$\GG = e^{-x} \,\hat{x} + e^{-y} \,\hat{y} +e^{-z} \,\hat{z}$
$\HH = yz\,\hat{x} + zx\,\hat{y} + xy\,\hat{z}$
$\II = x^2\,\hat{x} + z^2\,\hat{y} + y^2\,\hat{z}$
$\JJ = xy\,\hat{x} + xz\,\hat{y} + yz\,\hat{z}$
$\KK = s^2\,\hat{s}$
$\LL = r^3\,\hat{\phi}$
$\MM = r^3 \cos{\phi}\,\hat{r} + \frac{1}{r^2} \sin^2{\theta}\,\hat{\phi}$
- (DivergencePrism) Verify the Divergence Theorem on a prism.
Consider the vector field $\Vec F=(x+2)\hat{x} +(z+2)\hat{z}$.
Calculate the divergence of $\Vec F$.
In which direction does the vector field $\Vec F$ point on the plane $z=x$? What is the value of $\Vec F\cdot \hat n$ on this plane where $\hat n$ is the unit normal to the plane?
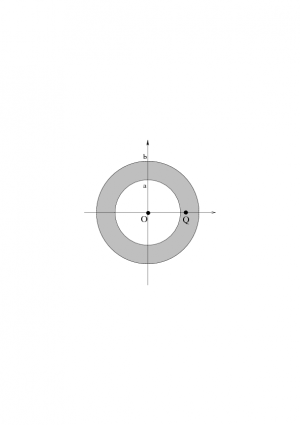
- (DivergenceSpherical) Verify divergence theorem for a spherical shell of matter, starting with an expression for the gravitational field.
The gravitational field due to a spherical shell of matter (or equivalently, the electric field due to a spherical shell of charge) is given by:
\begin{equation} \Vec g = \begin{cases}
0&\textrm{for } r<a\\ -G \,\frac{M}{b^3-a^3}\,\left( r-\frac{a^3}{r^2}\right)\, \hat r & \textrm{for } a<r<b\\
- G\,\frac{M}{r^2}\, \hat r & \textrm{for } r>b \\
\end{cases} \end{equation} (If you want extra practice with Gauss's law, this is a good question to practice on!)
This problem explores the consequences of the divergence theorem for this shell.
Using the given value of the gravitational field, find the divergence of the gravitational field everywhere in space. You will need to divide this question up into three parts: $r<a$, $a<r<b$, and $r>b$.
Discuss the physical meaning of the divergence in this particular example.
For this gravitational field, verify the divergence theorem on a sphere, concentric with the shell, with radius $Q$, where $a<Q<b$.
Discuss how this example would change if you were discussing the electric field of a uniformly charged spherical shell.
- (DivergencePractice2)
Choose some simple vector fields of your own and find the divergence of them both by hand and using Mathematica or Maple. Choose some that are written in terms of rectangular coordinates and others in cylindrical and/or spherical.
- (DivergenceVisualizePractice)
If you need more practice visualizing divergence, go through the Mathematica notebook on the course website.