You are here: start » activities » guides » osenergydiagramsim
Navigate back to the activity.
Energy Diagram Analysis: Instructor's Guide
Main Ideas
- Reasoning qualitatively from graph
- Understanding the relationships between kinetic energy, potential energy, and total energy on an energy diagram.
Students' Task
Estimated Time: 15 minutes
Students were presented with two potential energy vs. displacement graphs with the same amplitude and asked to determine which motion would have a greater period. 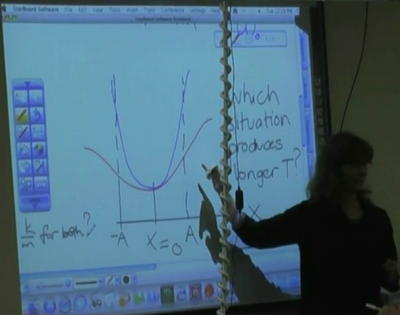
Prerequisite Knowledge
Knowledge of the basic algebraic form for kinetic energy, potential energy, and the total energy of a mass on a spring.
Props/Equipment
- Table top whiteboards and markers
Activity: Introduction
This activity begins with a demonstration from Simple Harmonic Oscillator. This simple demonstration provides a way to show how to obtain relevant information from a potential energy diagram.
After the explanation, students are given two different potential energy vs. displacement graphs: one parabolic and one sinusoidal, with the same curvature at the bottom (see picture above) and the same amplitude. Students then work in small groups to determine which motion would have a greater period.
This prompt is intentionally open ended in order to lead to deeper discussions. Students can be frustrated by the ambiguity of the problem, but it is a frustration that can lead to many productive discussions.
Activity: Student Conversations
What information do you need in order to determine the period?
- Many students will try to use the familiar expression $\omega = \sqrt{\frac{k}{m}}$ instead of gathering information from the given graph. Most of the students assume that both graphs represent a mass on a spring, so one of the ways to move them away from trying to reason from this equation is to remind the that only one of the graphs is a parabolic.
- Don't we need to know the mass of the systems to determine the period? It is a good idea to try to get the students to recognize that while we don't necessarily need to know the value of the mass, but we do need to make an assumption that the masses for both systems are equal in order to answer the original question. One way to do this is to ask them to consider what the graph can tell them for different assumptions about relative mass.
What information can the graph give you?
- This activity is done early enough in the Paradigms sequence that some students are still uncomfortable discussing the graph qualitatively, even once they realize that all that is needed is the distance and the speed.
- How do we find the speed? Most students recognize that since both systems have the same amplitude, a particle would go the same distance in both situations. However, they don't always recognize how to obtain the speed from an energy graph.
- What is the total energy of each system? Once students realize that they can find the speed from the kinetic energy, they will often ask what the total energy of each system is. It is better to ask students to try to answer this question themselves, to recognize that they can determine the relative total energy from the turning points.
Activity: Wrap-up
Things to emphasize:
- The relationships between kinetic energy, potential energy, and total energy in an energy diagram.
- What assumptions are necessary to gain the information you want from a graph.
Extensions
Depending on time and the conversations that arise, one can also ask students to consider constraints other than equal amplitude (e.g. equal mass, $m_1»m_2$, equal spring constant, equal total energy, etc.), in order to emphasize additional points.
- Some students want to assume that the total energy is the same for each system. If both systems were parabolic, one could still compare curvature in order to compare period. However, since one is parabolic and the other sinusoidal, one cannot actually make a definitive comparison.
- For two parabolic systems, it is not the mass or the spring constant that matters to the period, but the ratio of the two.
- What assumptions you make and how a graph is labeled has a great impact on what information you can glean from it.