You are here: start » activities » guides » cfballoon
Navigate back to the activity.
Visualizing Spherical Harmonics Using a Balloon: Instructor's Guide
Main Ideas
Spherical harmonics are continuous functions on the surface of a sphere.
The $\ell$ and $m$ values tell us how the function oscillates across the surface.
Spherical harmonics are complex valued functions.
Students' Task
Estimated Time: 30 min
Students set up a spherical coordinate system on a balloon, draw a spherical harmonic, and use the balloon as a prop to describe the main features of their spherical harmonic to the class.
Prerequisite Knowledge
Students should be familiar with the spherical coordinate system, and the equations describing spherical harmonics.
Props/Equipment
- Punch ball balloons (almost spherical), or standard party balloons (less perfect).
- White board markers
Activity: Introduction
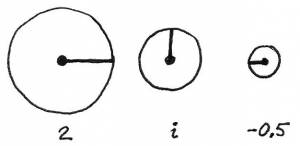
The instructor points out that visualizing complex numbers on a spherical surface is challenging, and then describes a way to visually represent a field of complex numbers. The visual representation is based on stylized Argand diagrams (examples below).
Note that the size of each circle represents magnitude, and the direction of the radial spoke represents phase.
Each small group is assigned a spherical harmonic from the list below:
- $(\ell = 1, m = 1)$
- $(\ell = 1, m = 0)$
- $(\ell = 1, m = -1)$
- $(\ell = 2, m = 1)$
- $(\ell = 2, m = 0)$
- $(\ell = 2, m = -1)$
There is room on the balloon to draw 8 complex numbers around the equator $(\theta = π/2)$. Similarly, complex numbers can be drawn around the balloon at $\theta = π/6$, $2π/6$, $4π/6,$ $5π/6$. Example below.
Groups work independently on their spherical harmonic.
Activity: Student Conversations
- During this time the Instructor and TA ask questions such as
- “Show me $\phi = 0$ on your sphere”
- “Show me $\theta = \pi/2$ on your sphere”
- ” Is your function well behaved (no discontinuities) everywhere on the surface?”
- If students need help with their coordinate system, ask them to draw a dot representing $\theta = 0$ and line to represent all points with $\phi = 0$.
- Not all students fully understand the stylized Argand diagrams, but most can still use them appropriately.
Activity: Wrap-up
After students have made their plots, each group shows the main features of their spherical harmonic. For example,
- Are there nodes at the poles?
- Does the phase wind up 360 degrees as we move around the equator?
- How is $m = 1$ different from $m = -1$?
Useful points to review are:
- Unless $m = 0$, the spherical harmonics must have nodes (zeros) at the $\theta = 0$ and $\theta = \pi$ to ensure a continuous function.
- The index $m$ is equivalent to the number of times the phase gets wound as you move around the equator.
What happens if we add two spherical harmonic functions? For example ($/ell = 1$, $m = 1$) and ($\ell = 1$ $m = -1$). Discuss the constructive and destructive interference of complex numbers.
Extensions
- What linear combination of the $\ell = 0$ and $\ell=1$ spherical harmonics would describe a probability density that is big in the northern hemisphere and small in the southern hemisphere?
- What linear combination of the $\ell = 0$ and $\ell = 1$ spherical harmonics would describe a probability density that is big in the $x$direction but and small in $-x$ direction?
An alternative activity only asks students to show how the phase (not the magnitude) changes about the equator. Have one group at each table show $e^{i\phi}$ and one group show $e^{-i\phi}$ around the equator. By asking them to then add their functions together, you can use this as a way of introducing the superposition of states and to talk about how physicists' counting of states ($p_1$, $p_0$, $p_{-1}$) differs from chemists' counting of states ($p_x$, $p_y$, $p_z$).