Two Coupled Oscillators (30 minutes)
Before beginning this activity, it is recommended that the instructor ask the Single Simple Harmonic Oscillator small whiteboard question. This is useful for reviewing Hooke's Law and how to use the law to find the equations of motion for an oscillating system.
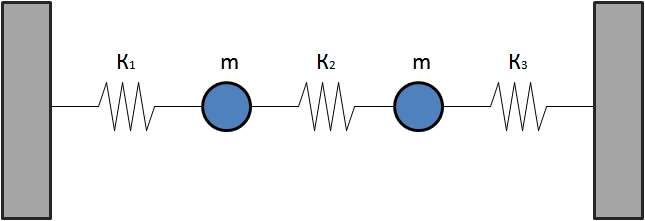
- Draw the following diagram on the board for the class:
Be sure to define the positive direction of displacement for the problem; this decision will directly influence the proper signs for the equations of motion.
- The key difference between analyzing a single oscillator and any coupled oscillator is the equations of motion for each particle will also have dependence on the displacement of neighboring particles.
- Ask the students what the equation of motion for each particle will look like. Work through any student's answer to find the equations:
$$Force \, on \, 1 \, = \, m\frac{d^{2}x_{1}}{dt^{2}} \, = \; - \kappa_{1}x_{1} + \kappa_{2} \left( x_{2}-x_{1}\right)$$
and
$$Force \, on \, 2 \, = \, m\frac{d^{2}x_{2}}{dt^{2}} \, = \; - \kappa_{3}x_{2} - \kappa_{2} \left( x_{2}-x_{1} \right) \; \; . $$
- Now, what $x_{1}(t)$ and $x_{2}(t)$ will satisfy these equations? Let's look for solutions for normal modes (that is, for solutions where all atoms oscillate with the same frequency). In polar form, these solutions will have the general form
$$x_{1}(t)=Re\left[Ae^{i \omega t} \right]$$
and
$$x_{2}(t)=Re\left[Be^{i \omega t} \right] \; \; ,$$
where A and B are complex constants that will help correct for any phase differences between the particles.
- We can now insert these solution forms into our differential equations of motion to find more information about $\omega$, A, and B (Do this for the class, and factor out a term of $e^{i \omega t}$ from each equation). After factoring out our frequency term, our expressions reduce to a set of coupled linear equations of the form:
$$-m\omega^{2}A=-\kappa_{1}A + \kappa_{2}B - \kappa_{2} A $$
and
$$-m\omega^{2}B=-\kappa_{3}B - \kappa_{2}B + \kappa_{2} A \; \; .$$
- It will be easier to gather more information about the frequency by representing these equations in terms of matrices. This is done as so:
$$m\omega^{2}\left[\begin{array}{c} A\\ B\\ \end{array}\right] \; = \; \left[\begin{array}{cc} \left(\kappa_{1}+\kappa_{2}\right) & -\kappa_{2} \\ -\kappa_{2} & \left(\kappa_{2}+\kappa_{3}\right)\\ \end{array}\right] \left[\begin{array}{c} A\\ B\\ \end{array}\right] \; \; . $$
Now, with our expression in matrix notation, the eigenvalues of the matrix on the right-hand side will directly lead to the solution for the normal mode frequencies. To find the eigenvalues, we perform the operation
$$det\left(A-\lambda I\right) \; = \; \left|\begin{array}{cc} \kappa_{1}+\kappa_{2}- \lambda & -\kappa_{2} \\ -\kappa_{2} & \kappa_{2}+\kappa_{3} - \lambda \\ \end{array}\right| \; \; . $$
- Let's consider the special case where $\kappa_{1}=\kappa_{2}=\kappa_{3}=\kappa$. For this condition, the determinant yields the expression
$$\left(2\kappa - \lambda\right)^{2} - \kappa^{2}= 0 \; \; , $$ $$2\kappa - \lambda= \pm \, \kappa \; \; , $$ $$\lambda = 2\kappa \; \pm \; \kappa \; \; .$$
Now, each eigenvalue of $\lambda$ must correspond to a particular value for $\omega$ in our original matrix notation. This is expressed mathematically as
$$m\omega^{2}=\kappa \; or \; 3\kappa \; \; .$$
We can see from this expression that our normal mode frequencies are
$$\omega_{-} \, = \, \sqrt{\frac{\kappa}{m}}$$
and
$$\omega_{+} \, = \, \sqrt{\frac{3\kappa}{m}} \; \; , $$
and by inserting these frequencies into our original linear equations, it can be easily shown that:
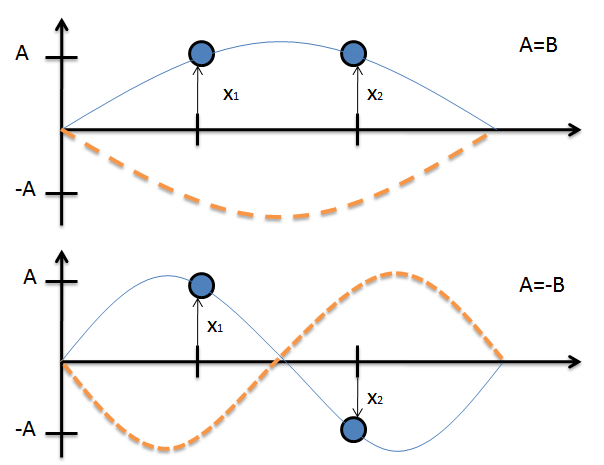
$$for \; \omega_{-} \; , \; A=B$$
and
$$for \; \omega_{+} \; , \; A=-B \; \; . $$
Now, we have the needed information to draw the envelope functions for each normal mode in this system.
Some important observations for each wave function:
- The envelope is a standing wave for both cases.
- The wavelength for the second envelope function is twice the wavelength of the first.
- The frequency of oscillation for each particle is equal to the envelope function's frequency.
- $\omega \neq vk$, where $k$ is the wave vector of the envelope function. Effectively, the fact that the wavelength of the second envelope function is twice that of the first does not imply that the same relation will hold for the frequencies of each envelope function.