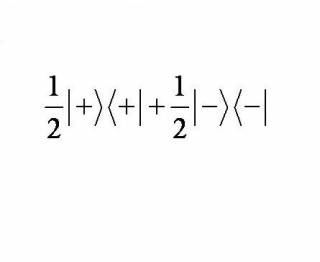You are here: start » activities » main
Describing the Sample Oven in the Stern-Gerlach Experiment Mathematically
Highlights of the activity
- For this activity, the instructor claims:
The oven is the superposition of the outer product: $\; \; \frac{1}{2} \; \vert +\rangle\langle+\vert \; + \; \frac{1}{2} \; \vert- \rangle\langle -\vert$.
- The students must then determine if the instructor's claim is true, and why or why not, by using the density matrix to calculate the probability of finding a sample coming out of the Stern-Gerlach oven in either the spin up or spin down state with x, y, or z orientation.
Reasons to spend class time on the activity
Up to this point in the course, most scenarios posed provided the initial quantum state of whatever is being observed. However, in situations when the initial quantum state being measured is not known definitively, it must be described as a mixed state, or a collection of quantum states characterized by how probable they are. This activity introduces students to the density operator's mathematical definition and challenges students to think about how the density operator can be used to compute the probability of a mixed state being measured in a particular state.