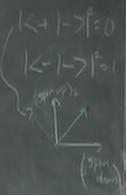You are here: start » courses » lecture » splec » splecdfindspinupx
Deriving Spin-up with x-direction in the z-basis (25 minutes)
- After showing that $\vert+ \rangle$ and $\vert- \rangle$ form a complete basis in the two-dimensional vector space the kets live in, tell the students we should be able to find $\vert+ \rangle_{x}$ in terms of $\vert+ \rangle$ and $\vert- \rangle$. So, $\vert+ \rangle_{x}$ has the general form:
$$\vert+ \rangle_{x}=a \vert+ \rangle + b\vert- \rangle \; \; .$$
- Now, a graphical representation of the linear combinations and orthogonality of the different kets is useful for students to visualize what's occuring in this two-dimensional vector space.
Note that the white arrows represent $|+ \rangle$ and $|- \rangle$ while the green arrows represent $\vert+ \rangle_{x}$ and $\vert- \rangle_{x}$. However, we have no more room in our two-dimensional vector space to properly draw $\vert+ \rangle_{y}$ and $\vert- \rangle_{y}$ in a manner that reflects the results of the Stern-Gerlach experiment and the orthogonality conditions. The way out of this is with complex numbers. Thus, the coefficients of $\vert + \rangle _{x}$ are inherently complex. We should actually represent our $\vert+ \rangle_{x}$ state as
$$\vert+ \rangle_{x}=A \vert+ \rangle + B\vert- \rangle \; \; $$
where a and b are the real parts of A and B.
- Now, to find a and b for $\vert+ \rangle_{x}$, tell students to use the results from yesterday's experiment. Write down that the experiment performed can be represented as
$$\langle +\vert+ \rangle_{x}=\langle +\vert A \vert+ \rangle + \langle +\vert B\vert- \rangle \; \; , $$
$$\langle +\vert+ \rangle_{x}=A \langle +\vert + \rangle + B\langle +\vert- \rangle \; \; , $$
$$\langle +\vert+ \rangle_{x}=A \; \; .$$
- The students experimentally found that the probability that a particle prepared in the $\vert+ \rangle_{x}$ state would leave a z-oriented S.G. device as $\vert+ \rangle$ was $\frac{1}{2}$. So, writing this down in terms of the fourth postulate of quantum mechanics will yield
$$\left\vert\langle +\vert+ \rangle_{x}\right\vert^{2}=\vert A\vert^{2}=\frac{1}{2} \; \; . $$
The same can be done to find b by performing the measurement $\langle -\vert+ \rangle_{x}$ to find
$$\left\vert\langle -\vert+ \rangle_{x}\right\vert^{2}=\vert B\vert^{2}=\frac{1}{2} \; \; . $$
- This is an excellent place to perform the Finding the Square of a Norm of a Complex Number activity to have students find that if $A=ae^{i \alpha}$, then
$$\left\vert A\right\vert^{2}=a^{2}$$
- Now, our state $\vert+ \rangle_{x}$ can be represented explicitly in terms of complex numbers as
$$\vert+ \rangle_{x}=\frac{1}{\sqrt{2}}e^{i \alpha} \vert+ \rangle + \frac{1}{\sqrt{2}}e^{i \beta}\vert- \rangle \; \; . $$
State that in quantum mechanical experiments, overall phases do not affect the experimental results. Thus, the only important value is the relative phase between $e^{i \alpha}$ and $e^{i \beta}$. Choose $\alpha=0$ to make the first term real, and the expression becomes
$$\vert+ \rangle_{x}=\frac{1}{\sqrt{2}} \vert+ \rangle + \frac{1}{\sqrt{2}}e^{i \beta}\vert- \rangle \; \; . $$
The same process can be performed with $\vert- \rangle_{x}$ to find that
$$\vert- \rangle_{x}=\frac{1}{\sqrt{2}} \vert+ \rangle + \frac{1}{\sqrt{2}}e^{i \delta}\vert- \rangle \; \; . $$
* Now, we need to find how the two phases are related. We can use the fact that the two states are orthogonal to each other, that is that $\left\vert_{x}\langle -\vert+ \rangle_{x}\right\vert^{2}=0$ (be sure to note that the coefficients in $_{x}\langle -\vert$ are the complex conjugate of $\vert- \rangle_{x}$) . This is a good time to have students perform the Calculating $_{x}\langle -\vert+ \rangle_{x}$ activity. Doing so will give
$$\frac{1}{4}\left\vert1+e^{i (\beta - \delta)}\right\vert^{2}= 0 \; \; . $$
- After taking the square of the norm above and dividing out the $\frac{1}{4}$, this is an excellent time to review Euler's Identity and how cosine is represented in complex terms (make it a small white board question if you wish). Point out that the $e^{i (\beta - \delta)}+e^{-i (\beta - \delta)}$ term is $2cos(\beta - \delta)$.
- Finally, if $2cos(\beta - \delta)=-2$, then $\beta - \delta = \pi$. Now, we are free to choose that $\beta=0$ because the relative phase is what is important for this case. Warn the students that this is a very special case where we can pick one of the phase angles, and that students should be very cautious when picking the phase angle arbitrarily. So,
$$\beta = 0$$
and
$$\delta = -\pi \; \; .$$
- Inserting values for $\beta$ and $\delta$ into the original kets will yield the answers
$$\vert+ \rangle_{x}=\frac{1}{\sqrt{2}} \vert+ \rangle + \frac{1}{\sqrt{2}}\vert- \rangle \; \; . $$
and
$$\vert- \rangle_{x}=\frac{1}{\sqrt{2}} \vert+ \rangle - \frac{1}{\sqrt{2}}\vert- \rangle \; \; . $$