Table of Contents
Conservative Fields
Prerequisites
Students should be able to:
- Find $d\vec{r}$ for a straight or curved path.
- Evaluate the dot product between two vectors qualitatively.
- Read vector field maps.
- Use chop-multiply-add ideas to construct an integral.
- Estimate integrals by approximation.
Reading: GVC § Independence of Path–Finding potential Functions
In-class Content
- Counting Paths (SGA - 30 min)
- Lecture - 20 min
- What is the difference between the line integral and the flux integral (given that both use the dot product)?
- What does it mean for a field to be conservative?
- Path independent
- Corresponds to a surface (scalar field) that it is the gradient of
- Is curl free Note: Curl is needed for 3 different ideas in this class: Conservative Work, Going from $\vec A$ to $\vec B$, and getting from $\vec B$ to $\vec J$.
- QUIZ
- Lecture - 10 min
Optional In-class Content
- Murder Mystery Method (SGA - 50 min) (alternatively a homework problem - see below)
- Conservative Fields (lecture) (Math 3.5: Independence of Path, Math 3.6: Conservative Vector Fields, Math 3.7: Finding Potential Functions)
- Equivalent Statements (lecture)
Homework for Static Fields
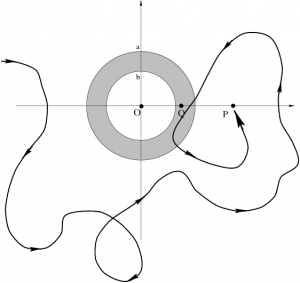
- (PathIndependence) Students explicitly compute the work required to bring a charge from infinity using two different paths. Include part (e) as an additional path that cannot be solved by integration. (You must invoke path-independence of conservative fields.)
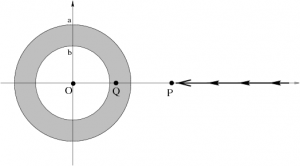
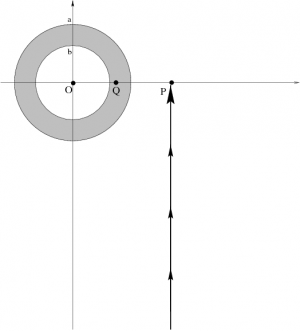
The gravitational field due to a spherical shell of mass is given by: %/* \[ \Vec g =\begin{cases}
0&r<b\\
-\frac{4}{3}\pi\rho\,G\left({r}-{b^3\over r^2}\right)\hat{r}&b<r<a\\ -\frac{4}{3}\pi\rho\, G\left({a^3-b^3\over r^2}\right)\hat{r}&a<r\\
\end{cases}\]
where $b$ is the inside radius of the shell, $a$ is the outside radius of the shell, and $\rho$ is the constant mass density.
Using an explicit line integral, calculate the work required to bring a test mass, of mass $m_0$, from infinity to a point $P$, which is a distance $c$ (where $c>a$) from the center of the shell.
Using an explicit line integral, calculate the work required to bring the test mass along the same path, from infinity to the point $Q$ a distance $d$ (where $b<d<a$) from the center of the shell.
Using an explicit line integral, calculate the work required to bring the test mass along the same radial path from infinity all the way to the center of the shell.
Using an explicit line integral, calculate the work required to bring in the test mass along the path drawn below, to the point $P$ of question a. Compare the work to your answer from question a.
What is the work required to bring the test mass from infinity along the path drawn below to the point $P$ of question a. Explain your reasoning.
- (MurderMystery) This question is adapted from the in-class activity
(Throughout this problem, assume all of the constants-including invisible factors of 1-carry the necessary dimensions so that the fields in this problem are dimensionally correct.) Consider the vector field in rectangular coordinates: $$\vec{E} = \frac{q}{4 \pi \epsilon_{0}} [(2 x y^3z+z)\hat{x} + (3x^2 y^2 z) \hat{y}+(x^2 y^3+x)\hat{z}]$$
Using only the $x$-component of $\vec{E}$, find as much information as possible about the potential from which this electric field might have come.
Repeat this exercise for the $y$- and $z$-components of $\vec{E}$. Does this field come from a potential?
Consider the different vector field: $$\vec{E} = \frac{q}{4 \pi \epsilon_{0}} (-y \hat{x} + x \hat{y})$$ Does this field come from a potential?
Consider the different vector field: $$\vec{E}=\frac{q}{4 \pi \epsilon_{0}} \left(s \hat{\phi}\right)$$ Does this field come from a potential?