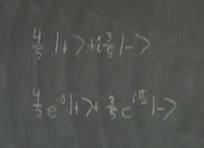Tell the students to draw a diagram of each component in the complex plane if they're struggling to identify the relative phase. The relative phase will be the angle difference between the two points in the complex plane.
Be sure to re-emphasize that relative phases in quantum states do matter. The overall phases do not play a role in probability calculations, but relative phases will change results significantly.
If students are still confused as to why overall phases do not matter, write down a general expression with the coefficients in polar form for a state $\vert\psi \rangle$ and multiply both sides by an arbitrary phase. Calculate the probability of measuring $\vert+ \rangle$ to show that taking the square of the norm for the probability calculation will make the overall phase term disappear.