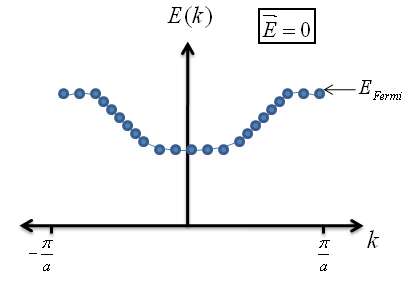
Let's now consider a crystal that has a filled band. Equivalently, let's consider a crystal that has an electron filling each possible eigenstate the crystal has to offer.

Just as with the half-filled band, some of the electrons are moving left while some are moving right. However, the total net transfer of charge is zero because each electron with equal positive and negative $k$ values cancel each other's momentum.

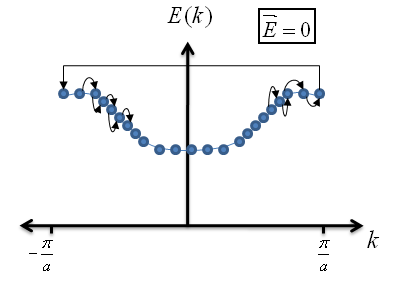
Now, let's see what happens when an electric field is applied to the crystal.

In this case, all of the electrons are accelerated. However, once an electron reaches $k=\frac{\pi}{a}$, it is actually moving into an identical state as $k=-\frac{\pi}{a}$. The electrons do move, but all they do is cycle through the possible energy states in the crystal; thus, the net transfer of charge is zero. This crystal is an insulator.