- §1. Harmonic Integrals
- §2. Completeness
- §3. Finding Coefficients
- §4. Example
- §5. The Gibbs Phenomenon
- §6. Symmetries
Example
Let's consider an example. Suppose $f(x)$ describes a square wave, so that \begin{equation} f(x) = \begin{cases} C & (0\le x<\frac{L}{2}) \\ 0 & (\frac{L}{2}<x\le L) \end{cases} \end{equation} (the value of $f$ at $x=L/2$ doesn't matter). According to the results of the previous sections, we have \begin{equation} f = \frac12 a_0 + \sum_{m=1}^\infty a_m \cos\left(\frac{2\pi m x}{L}\right) + \sum_{m=1}^\infty b_m \sin\left(\frac{2\pi m x}{L}\right) \end{equation} where \begin{align} a_0 &= \frac{2C}{L} \int_0^{\frac{L}{2}} dx = C,\\ a_m &= \frac{2C}{L} \int_0^{\frac{L}{2}} \cos\left(\frac{2\pi mx}{L}\right) \,dx = 0 ,\\ b_m &= \frac{2C}{L} \int_0^{\frac{L}{2}} \sin\left(\frac{2\pi mx}{L}\right) \,dx = \begin{cases} \frac{2C}{\pi m} & \hbox{($m$ odd)} \\ 0 & \hbox{($m$ even)} \end{cases} \end{align} Putting this all together, \begin{equation} f = C + \sum_{\substack{m=1\\ m\hspace{1.5pt}\mathrm{odd}}}^\infty \frac{2C}{\pi m} \sin\left(\frac{2\pi mx}{L}\right) . \end{equation} It is instructive to plot the first few terms of this Fourier series and watch the approximation improve as more terms are included, as shown in Figure 1.
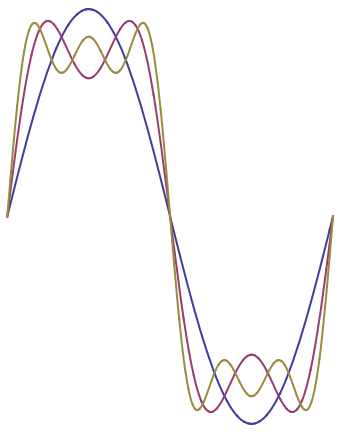
Figure 1: The first few partial sums in the Fourier series for a step function.