You are here: start » book » content » timelength
We have seen that the postulates of relativity force the surprising conclusion that time is observer-dependent. We now examine this phenomenon in more detail.
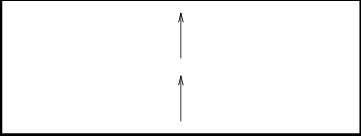
Consider again a train, of height $h$, with a beam of light bouncing up and down between mirrors on the floor and ceiling, as shown in the first sketch in Figure 2.4. The time between bounces can be interpreted as the “ticks” of a clock, and of course this interval, as measured on the train, is independent of whether the train is moving. However, as shown in the second sketch, a stationary observer sees something quite different.
From the ground, the light appears to move diagonally, and hence travels a longer path than the vertical path seen on the train. But since the light must move at the same speed for both observers, each “tick” takes longer according to the ground-based observer than for the observer on the train. Thus, the observer at rest sees the “clock” of the moving observer run slow!
Work through each step of this argument carefully; the key assumption is Postulate II, namely that the light must travel at the same speed for both observers. This is not the behavior we expect from our daily experience!
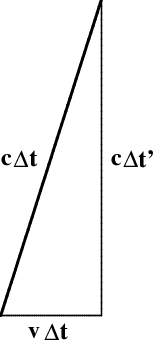
To compute how the times are related, we must first introduce some notation. Let $t$ denote time as measured on the ground, and $t'$ denote time as measured on the train; we will similarly use $x$ and $x'$ to measure length. One tick of the clock as seen on the train takes time $\Delta t'$, where \begin{equation} h = \cc \,\Delta t' \label{height} \end{equation} Suppose the same tick takes time $\Delta t$ as seen from the ground. In this time, the light travels a distance $\cc \,\Delta t$, which is the hypotenuse of a right triangle with legs $h$ and $v\,\Delta t$. As shown in Figure 2.5, the Pythagorean Theorem now leads to \begin{equation} (\cc \,\Delta t)^2 = (v \,\Delta t)^2 + h^2 \end{equation} which can be solved for $h$. Comparing the result with ($\ref{height}$), we obtain \begin{equation} \Delta t = \frac{1}{\sqrt{1-\vvcsq}} \>\Delta t' \label{time} \end{equation} which indeed shows that the moving clock runs slower than the stationary one ($\Delta t > \Delta t'$), at least for speeds $v<\cc$. The factor relating these times shows up so often that we give it a special name, defining \begin{equation} \gamma = \frac{1}{\gammainv} \end{equation}
This effect, called time dilation, has important consequences for objects traveling at a significant fraction of the speed of light, but has virtually no effect for objects at everyday speeds ($v\ll c$). It is this effect which allows cosmic rays to reach the earth — the particles' lifetimes, as measured by their own clocks, is many orders of magnitude shorter than the time we observe them traveling through the atmosphere.
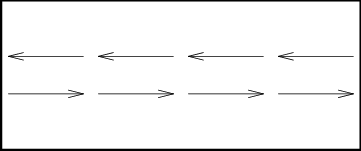
Time is not the only thing on which observers do not agree. Consider now a beam of light bouncing horizontally between the front and back of the train, as shown in the first sketch in Figure 2.6. As seen on the train, if it takes time $\Delta t'$ to make a round trip, and the length of the train is $\Delta x'$, then we must have \begin{equation} \cc \,\Delta t' = 2 \,\Delta x' \label{length} \end{equation}
What does the observer on the ground see? Don't forget that the train is moving, so that, as shown in the second sketch, the distance traveled in one direction is different from that in the other. More precisely, light starting from the back of the train must “chase” the front; if it takes time $\Delta t_1$ to catch up, then the distance traveled is $\Delta x + v\,\Delta t_1$, the sum of the length of the train (as seen from the ground!)\ and the distance the front of the train traveled while the light was under way. Similarly, if the time taken on the return journey is $\Delta t_2$, then the distance traveled is $\Delta x - v\,\Delta t_2$. Thus, \begin{eqnarray} \cc \,\Delta t_1 &=& \Delta x + v \,\Delta t_1 \\ \cc \,\Delta t_2 &=& \Delta x - v \,\Delta t_2 \end{eqnarray} or equivalently \begin{eqnarray} \Delta t_1 &=& \frac{\Delta x}{\cc - v} \\ \Delta t_2 &=& \frac{\Delta x}{\cc + v} \end{eqnarray} Combining these results leads to \begin{eqnarray} \cc \,\Delta t &=& \cc \,\Delta t_1 + \cc \,\Delta t_2 \nonumber\\ &=& \frac{2\,\Delta x}{1-\vvcsq} \end{eqnarray} and comparing with ($\ref{time}$) and ($\ref{length}$) leads to \begin{equation} \Delta x = \gammainv \> \Delta x' = \frac{1}{\gamma} \,\Delta x' \end{equation} Thus, a moving object appears to be shorter in the direction of motion than it would be at rest; this effect is known as length contraction.