Colliding Particles III
A particle of mass $m$ whose total energy is twice its rest energy collides with an identical particle at rest. If they stick together, what is the mass of the resulting composite particle? What is its speed?
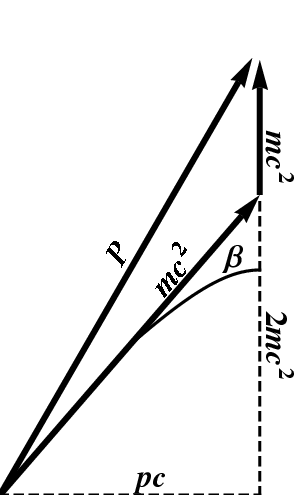 Figure 10.5: Spacetime diagram for the collision of identical particles.
Figure 10.5: Spacetime diagram for the collision of identical particles.
A momentum diagram for this collision is shown in Figure 10.5. The particle is shown moving to the right; its rest energy is given by the magnitude of the hypotenuse of the right triangle shown, and is of course $mc^2$. The observed energy is however $2mc^2$; this is the magnitude of the vertical leg of the triangle. The momentum vector of the second particle is vertical (since it is at rest), with magnitude $mc^2$ (the rest energy). Adding these two momentum vectors together yields the vector labeled $P$, whose vertical component is clearly $3mc^2$. What is its horizontal component? The same as the original momentum. We have \begin{equation} \cosh\beta = 2 \end{equation} and therefore \begin{equation} p = mc\sinh\beta = \sqrt{3}\,mc \end{equation} The rest energy of the resulting particle is therefore given by \begin{equation} M^2c^4 = (3 mc^2)^2 - (\sqrt{3}mc)^2 c^2 = 6\,m^2c^4 \end{equation} so that $M=\sqrt{6}m$. The speed of the resulting particle is obtained from \begin{equation} \frac{v}{c} = \tanh\alpha = \frac{pc}{E} = \frac{\sqrt{3}}3 \end{equation}