Exponentials (and Logarithms)
Hyperbolic trigonometric functions are usually defined using formulas (Equations (1) and (2) of §4.1) and it takes some work (and independent knowledge of the exponential function) to show directly that our definition is equivalent to this one. We turn this on its head and instead define \begin{equation} \exp(\beta) = \cosh\beta + \sinh\beta \label{expdef} \end{equation} The function $\exp(\beta)$ as defined in ($\ref{expdef}$) has an immediate geometric interpretation, as shown in Figure 15.1, where it is important to recall that $\beta$ is the hyperbolic angle defined above, not the Euclidean angle that would be measured by a (Euclidean) protractor.
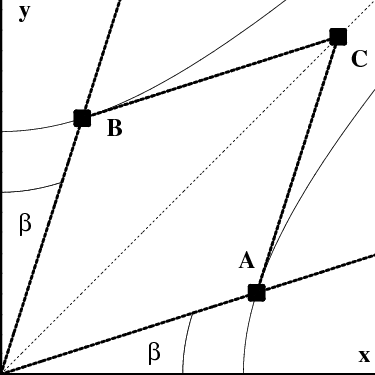
Figure 15.1: The geometric definition of $\exp(\beta)$.
We immediately have \begin{equation} d\Big(\exp(\beta)\Big) = \sinh\beta\,d\beta + \cosh\beta\,d\beta = \exp(\beta)\,d\beta \label{expdiff} \end{equation} but it remains to show that $\exp(\beta)$ as defined above is really the same as $e^\beta$. It is enough to show that $\exp(\beta)$ is an exponential function, that is, that it satisfies \begin{eqnarray} \exp(0) &=& 1 \label{expzero}\\ \end{eqnarray}\begin{eqnarray} \exp(u+v) &=& \exp(u)\,\exp(v) \label{expprop} \end{eqnarray} and to then define \begin{equation} e = \exp(1) \label{edef} \end{equation} Verifying that this definition of $e$ agrees with the usual one can then be established in several ways, such as by resorting to uniqueness results for solutions of differential equations.
First, however, we need to verify ($\ref{expzero}$) and ($\ref{expprop}$). The first of these conditions, ($\ref{expzero}$), follows immediately from the fact that $\beta=0$ corresponds to putting the point $A$ at $(\rho,0)$ in Figure 4.2. Examining ($\ref{expprop}$), we see that we need to know the addition formulas for the hyperbolic trigonometric functions, which we now construct. 1)
We first construct right triangles whose legs are not horizontal and vertical. Recall that the derivative of a vector of constant magnitude must be perpendicular to that vector, since \begin{equation} \vv\cdot\vv = \hbox{constant} \Longrightarrow 0 = d(\vv\cdot\vv) = 2\,\vv\cdot d\vv \label{vectorperp} \end{equation} Since the position vector to points on a circle centered at the origin has constant magnitude, we have shown that radii are orthogonal to circles. This argument holds just as well in hyperbola geometry, and establishes orthogonality between radial lines intersecting our hyperbolas, and the tangent lines to the hyperbolas at the point of intersection.
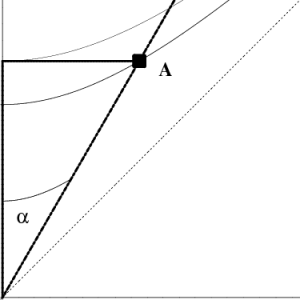

Figure 15.2: Using a shifted right triangle to represent the hyperbolic trigonometric
functions.
Consider now the situation shown in Figure 15.2. In the first drawing, the angle $\alpha$ is in standard position, leading to the right triangle shown, with radial leg $\rho\,\cosh\alpha$ and horizontal leg $\rho\,\sinh\alpha$. In the second drawing, the angle $\alpha$, has been shifted to the right, but since the hypotenuse and radial leg of the resulting right triangle have the same length as before, so must the remaining leg; the triangles in the two drawings are congruent in hyperbola geometry.

Figure 15.3: The geometric construction of the hyperbolic addition formulas.
Redraw the second drawing, as shown in Figure 15.3, so that point $B$ corresponds to angle $\beta$, and point $A$ corresponds to angle $\alpha+\beta$ (as measured from the $y$-axis). Thus, the coordinates of these points are given by \begin{eqnarray} B &=& (\rho\,\sinh\beta,\rho\,\cosh\beta) \nonumber\\ A &=& \Big(\rho\,\sinh(\alpha+\beta),\rho\,\cosh(\alpha+\beta)\Big) \end{eqnarray} Introduce the point $C$ as shown, so that the distance from the origin to $C$ is $\rho\,\cosh\beta$, that is, so that the coordinates of $C$ are given by \begin{equation} C = B \cosh\alpha \label{C1} \end{equation} But by the discussion of Figure 15.2 the other leg of the triangle has length $\rho\,\sinh\beta$, so that we must also have \begin{equation} C = A - B^\perp\sinh\alpha \label{C2} \end{equation} where \begin{equation} B^\perp = (\rho\,\cosh\beta,\rho\,\sinh\beta) = \frac{dA}{d\beta} \end{equation} denotes the direction tangent to the hyperbola at $B$. By comparing (\ref{C1}) with (\ref{C2}), we find that \begin{equation} A = B\,\cosh\alpha + B^\perp\,\sinh\alpha \end{equation} and we have established the addition formulas 2) \begin{eqnarray} \sinh(\alpha+\beta) &=& \sinh\alpha\cosh\beta + \cosh\alpha\sinh\beta \nonumber\\ \cosh(\alpha+\beta) &=& \cosh\alpha\cosh\beta + \sinh\alpha\sinh\beta \end{eqnarray} Returning to (\ref{expprop}), we finally have \begin{eqnarray} \exp(u+v) &=& \cosh(u+v) + \sinh(u+v) \nonumber\\ &=& \cosh(u)\cosh(v) + \sinh(u)\sinh(v) \\ && + \sinh(u)\cosh(v) + \cosh(u)\sinh(v) \nonumber\\ &=& \Big(\cosh(u)+\sinh(u)\Big) \Big(\cosh(v)+\sinh(v)\Big) \nonumber\\ &=& \exp(u)\,\exp(v) \nonumber \end{eqnarray} as desired.
A direct geometric verification is also possible, based on the construction in Figure 15.1, as shown in more detail in Figure 15.4. Denoting the origin by $O$, and noting that line $AD$ is at $45^\circ$, we see that the ratio of the length of $OD$ to that of $OA$ is precisely $\exp(\beta)$. In this sense, “rotation” through $\beta$ (taking $A$ to $D$) corresponds to stretching by a factor of $\exp(\beta)$. Composing two such “rotations” leads directly to ($\ref{expprop}$); the details are left to the reader.
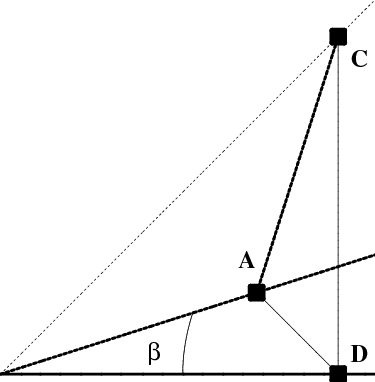
Figure 15.4: The geometric verification that “$\exp$” is exponential.
Having verified the desired properties of the exponential function, it is now straightforward to define logarithms as the inverse of exponentiation, that is to define $\log(u)$ by \begin{equation} v = \log(u) \Longleftrightarrow u = \exp(v) \label{logdef} \end{equation} and to establish that this definition leads to the usual properties of the natural logarithm.