What is the rapidity $\beta$? Consider an observer moving at speed $v$ to the right. This observer's world line intersects the hyperbola \begin{equation} \csq t^2 - x^2 = \rho^2 \qquad (ct>0) \end{equation} at the point $A=(\rho\,\sinh\beta,\rho\,\cosh\beta)$; this line has “slope” 1) \begin{equation} \vc = \tanh\beta \end{equation} as required. Thus, $\beta$ is nothing more than the hyperbolic angle between the $\cc t$-axis and the worldline of a moving object. As discussed in the preceding chapter, $\rho\beta$ turns out to be precisely the distance from the axis as measured along the hyperbola (in hyperbola geometry!). This was illustrated in Figure 5.2,
Consider therefore an object moving at speed $u$ relative to an observer moving at speed $v$. Their rapidities are given by \begin{eqnarray} \uc = \tanh\alpha \\ \vc = \tanh\beta \end{eqnarray} To determine the resulting speed with respect to an observer at rest, simply add the rapidities! One way to think of this is that you are adding the arc lengths along the hyperbola. Another is that you are following a (hyperbolic) rotation through a (hyperbolic) angle $\beta$ (to get to the moving observer's frame) with a rotation through an angle $\alpha$, as shown in Figure \ref{addition0}. In any case, the resulting speed $w$ is given by \begin{equation} \overc{w} = \tanh(\alpha+\beta) = \frac{\tanh\alpha+\tanh\beta}{1+\tanh\alpha\tanh\beta} = \frac{\uc+\vc}{1+\overcc{uv}} \end{equation} which is — finally — precisely the Einstein addition formula!
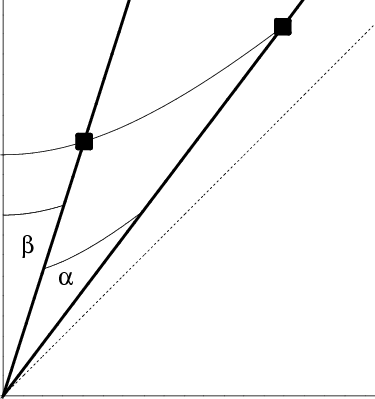
Figure 6.1: The geometry of the Einstein addition formula.