One twin travels 24 light-years to star X at speed ${24\over25}c$; her twin brother stays home. When the traveling twin gets to star X, she immediately turns around, and returns at the same speed. How long does each twin think the trip took?
Star X is 24 light-years away, so, according to the twin at home, it takes her 25 years to get there, and 25 more to return, for a total of 50 years away from earth. But the traveling twin's clock runs slow by a factor of $$\cosh\beta = \sqrt{1\over1-\tanh^2\beta} = {25\over7}$$ This means that, according to the traveling twin, it only takes her 7 years each way. Thus, she has only aged 14 years while her brother has aged 50!
This is in fact correct, and represents a sort of time travel into the future: It only takes the traveling twin 14 years to get 50 years into earth's future. (Unfortunately, there's no way to get back!)
But wait a minute. The traveling twin should see her brother's clock run slow, by the same factor of $25\over7$. So when 7 years of her time elapse, she thinks her brother has only aged ${49\over25}\approx2$ years! Her brother should therefore only have aged 4 years when she returns!
This can't be right. Either her brother is 4 years older, or he is 50 years older. Both siblings must surely agree on that!
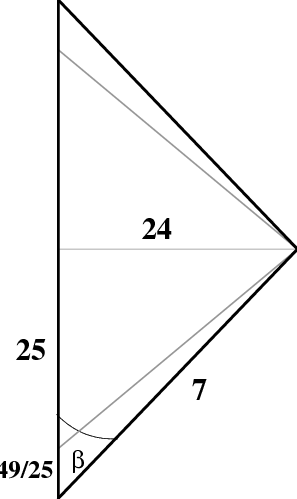
The easiest way to resolve this is to draw a single spacetime diagram showing the entire trip in the reference frame of the stay-at-home twin, as shown in Figure 8.2. The lower half of the figure is a hyperbolic triangle with $\tanh\beta=\frac{24}{25}$, and hypotenuse 7 years. The remaining diagonal lines are lines of constant time for the traveling twin, at the point of turnaround, while going and returning, respectively. There is another right triangle containing the hyperbolic angle $\beta$; the right angle is at the point of turnaround, and the hypotenuse is $\frac{7}{\cosh\beta}=\frac{49}{25}$ years, the age of the stay-at-home twin “when” the traveling twin turns around.
How much does each twin age? Simply measure the length of their world lines! Intervals are invariant; it doesn't matter how you compute them. The clear answer is that the brother has indeed aged 50 years, while the sister has only aged 14 years.
So what was wrong with the argument that the brother should have only aged 4 years? There are really 3 reference frames here: earth, going, and returning. The “going” and “returning” frames yield different times on earth for the turnaround — and these times differ by precisely ${1152\over25}\approx46$ years! From this point of view, it takes the traveling twin 46 years to turn around!
One difference between the twins is that the traveling twin is not in an inertial frame — she is in two inertial frames, but must accelerate in order to switch from one to the other. This breaks the symmetry between the two twins.
However, this is not really the best way to explain this paradox. It is possible to remove this particular asymmetry by assuming the universe is closed, so that the traveling twin doesn't need to turn around! A simplified version of this is to put the problem on a cylinder [ 8 ]. It turns out that this introduces another sort of asymmetry, but there is a simpler way to look at it.
The amount an observer ages is just the timelike interval measured along his or her worldline. We used this argument above. This approach also works for curved worldlines, corresponding to noninertial observers — except that one must integrate the infinitesimal timelike interval $d\tau=\sqrt{dt^2-ds^2}$ along the worldline.
A little thought leads to the following remarkable result: The timelike line connecting two events (assuming there is one) is the longest path from one to the other. (Think about it. Use this line as the $t$ axis. Then any other path has a nonzero contribution from the change in $x$ — which decreases the hyperbolic length of the path, and hence the time taken.)