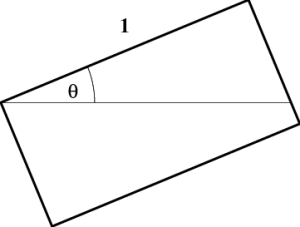
Consider the rectangular object of width 1 meter shown in the first sketch in Figure 3.6, which has been rotated so as to be parallel to the primed axes. How wide is it? As worded, this question is poorly posed. If width means “extent in the $x'$ direction”, then of course the answer is 1 meter. If, however, width means “extent in the $x$ direction”, then the answer is obtained by measuring the horizontal distance between the sides of the rectangle, which results in a value larger than 1. (The exact value is easily seen to be $1/\cos\theta$.)
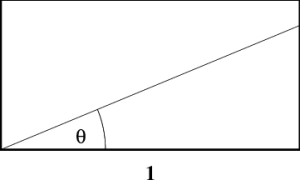
Repeat this exercise in the opposite direction. Take the same rectangular object, but orient it parallel to the unprimed axes, as shown in the second sketch. How wide is it? Clearly the “unprimed” width is 1 meter, and the “primed” width is larger (and again given by $1/\cos\theta$).
In one of the cases above, the “primed” width is smaller, yet in the other the “unprimed” width is smaller. What is happening here? If you turn your suitcase at an angle, it is harder to fit under your seat! It has, in effect, become “longer”! But which orientation is best depends, of course, on the orientation of the seat!
Remember this discussion when we address the corresponding questions in relativity in subsequent chapters.