Consider the head-on collision of 2 identical particles each of mass $m$ and energy $E$.
- In Newtonian mechanics, what multiple of $E$ is the energy $E'$ of one particle as observed in the reference frame of the other?
- In special relativity, what is the energy $E'$ of one particle as observed in the reference frame of the other?
- Suppose we collide 2 protons ($mc^2=1 \hbox{ GeV}$) with energy $E=30 \hbox{ GeV}$. Roughly what multiple of $E$ is $E'$ in this case?
1. In the center-of-mass frame, each particle has (Newtonian) kinetic energy \begin{equation} E = {1\over2}mv^2 \end{equation} In the reference frame of one of the particles, the other is moving twice as fast, so that \begin{equation} E' = {1\over2}m(2v)^2 = 4E \end{equation}
2. Now we must use the relativistic energy \begin{equation} E = mc^2\cosh\alpha \end{equation} In the reference frame of one of the particles, the other is not moving twice as fast. Rather, the hyperbolic angle has doubled. Thus \begin{equation} E' = mc^2\cosh(2\alpha) = mc^2 (2\cosh^2\alpha -1) \end{equation} so that \begin{equation} {E'\over E} = {2\cosh^2\alpha -1\over\cosh\alpha} \end{equation} The corresponding momentum diagrams are shown in Figure 10.2 in both frames of reference.
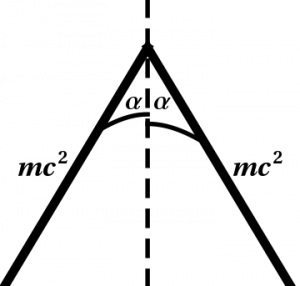

Figure 10.2: Momentum diagrams for the collision of identical particles, drawn both in
the center-of-mass frame (left) and in the frame of the right-hand particle
(right). In both cases, the dashed line represents the worldline of an
observer in the center-of-mass frame.
3. We are given that \begin{equation} \cosh\alpha = {E\over mc^2} = 30 \end{equation} so that \begin{equation} {E'\over E} = {2\cosh^2\alpha -1\over\cosh\alpha} \approx 60 \end{equation}