The hyperbolic trigonometric functions are usually defined using the formulas \begin{eqnarray} \cosh\beta &=& \frac{e^\beta + e^{-\beta}}{2} \label{coshdef}\\ \end{eqnarray}\begin{eqnarray} \sinh\beta &=& \frac{e^\beta - e^{-\beta}}{2} \label{sinhdef} \end{eqnarray} and then \begin{equation} \tanh\beta = \frac{\sinh\beta}{\cosh\beta} \end{equation} and so on. We will discuss an alternative definition below. The graphs of these functions are shown in Figure 4.1.
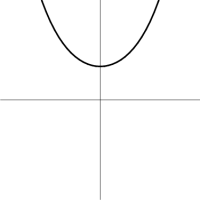


Figure 4.1: The graphs of $\cosh\beta$, $\sinh\beta$, and $\tanh\beta$, respectively.
It is straightforward to verify from these definitions that \begin{eqnarray} \cosh^2\beta - \sinh^2\beta &=& 1 \label{hyper}\\ \end{eqnarray}\begin{eqnarray} \sinh(\alpha+\beta) &=& \sinh\alpha\cosh\beta + \cosh\alpha\sinh\beta \label{sinh}\\ \end{eqnarray}\begin{eqnarray} \cosh(\alpha+\beta) &=& \cosh\alpha\cosh\beta + \sinh\alpha\sinh\beta \label{cosh}\\ \end{eqnarray}\begin{eqnarray} \tanh(\alpha+\beta) &=& \frac{\tanh\alpha+\tanh\beta}{1+\tanh\alpha\tanh\beta} \label{tanh}\\ \end{eqnarray}\begin{eqnarray} \frac{d}{d\beta} \sinh\beta &=& \cosh\beta \\ \end{eqnarray}\begin{eqnarray} \frac{d}{d\beta} \cosh\beta &=& \sinh\beta \end{eqnarray} A geometric derivation of these properties is given in Chapter 15.
The properties of the hyperbolic trigonometric functions look very much like their ordinary trigonometric counterparts (except for signs). This similarity derives from the fact that \begin{eqnarray} \cosh\beta &\equiv& \cos(i\beta) \\ \end{eqnarray}\begin{eqnarray} \sinh\beta &\equiv& -i\sin(i\beta) \end{eqnarray}