In this page, we will define vector field, divergence and
cross product and introduce gradient vector fields and curl
vector fields.
If to each point (x, y, z) of a domain D in the space a vector v =
v(x, y, z) is assigned, then a vector field is said to be given
in D.
Each vector v is regarded as to attach to the corresponding point
(x, y,
z). A good example of vector fields is the gravitational force. It attaches
a vector representing the direction and magnitude of gravity to each point
in
the space.
- Example 1
Let F denote the gravitational force exerted on a partical of mass
m at
P(x, y, z) by a mass M concentrated at the origin. Newton's law of gravitation
gives
where
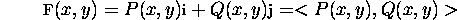= xi + yj + zk is the vector from origin
to P, r is its magnitude
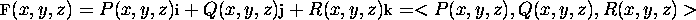and k is a universal
constant. See the graph below for the vector field
F.
- Example 2
Let F be the vector field
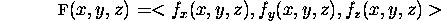
This is illustrated in the following two graphs around the neighbourhoods
of
(1, 0) and (-1, 0) and can be interpreted as the electric force
field due to two infinite straight wires, perpendicular to the xy plane at
(1, 0) and (-1, 0), homogeneously and oppositely charged with electricity.
Note that the second graph below is the zoom in around (1, 0) of
the first
graph.
For each vector field F = Pi + Qj + Rk
in a domain D,
if all P, Q, R have first partial derivatives in D, its divergence
div
F is defined as :
- Example 3
Let F = xyi + 2yj + xzk, then
div F = y + 2 + x.
The divergence has a definite physical significance. In fluid dynamics
it
appeara as a measure of the rate of decease of density at a point. The
divergence also play an important part in the theory of electromagnetic
fields. It has the following properties:
There are vector fields derived from differentiable functions of
multivariable. Let f(x, y, z) be a differentiable function of three
variables, then its gradient vector field is defined as
- Example 4
Let T(x, y, z) = xyz be a function giving temperature at the point (x, y,
z).
Its gradient vector field grad T = yzi + xzj + xyk shows
the
direction at the position (x, y, z) and the rate, magnitude of gradient
, in which the temperature increases the fast.
The cross product between vector fields and/or vectors could
produce
vector fields. The definition of cross product is as follows:
Let A = ai + bj + ck and B = di
+ ej
+ fk, then their cross product is defined as
- Example 5
Let A = i and B = j,
Clearly, their cross product vector k is perpendicular to
both A
and B. In fact, this is one of the important properties of cross
product among the following:
The curl vector field of the vector field F = Pi +
Qj
+ Rk is defined as:
when all P, Q, R have first partial derivatives.
The curl is important in the analysis of the velocity fields of fluid dynamics
and in the analysis of electromagnetic force fields. The curl can be
interpreted as measuring angular motion of a fluid and the condition curl
F = 0 for a velocity field F characterizes what are termed
irrotational flows. The analogous equation curl E = 0
for the
electric force vector E holds when only electrostatic forces are
present. The curl satisfies the basic laws:
